
【題目】如圖,直線y=﹣x+5與x軸交于點B,與y軸交于點D,拋物線y=﹣x2+bx+c與直線y=﹣x+5交于B,D兩點,點C是拋物線的頂點.

(1)求拋物線的解析式;
(2)點M是直線BD上方拋物線上的一個動點,其橫坐標為m,過點M作x軸的垂線,交直線BD于點P,當線段PM的長度最大時,求m的值及PM的最大值;
(3)在拋物線上是否存在異于B、D的點Q,使△BDQ中BD邊上的高為3![]() ,若存在求出點Q的坐標;若不存在請說明理由.
,若存在求出點Q的坐標;若不存在請說明理由.
【答案】(1)拋物線的表達式為:y=﹣x2+4x+5;(2)當m=![]() 時,PM有最大值
時,PM有最大值![]() ;(3)存在滿足條件的點Q,其坐標為Q1(2,9),Q2(3,8),Q3(﹣1,0),Q4(6,﹣7).
;(3)存在滿足條件的點Q,其坐標為Q1(2,9),Q2(3,8),Q3(﹣1,0),Q4(6,﹣7).
【解析】
(1)y=-x+5,令x=0,則y=5,令y=0,則x=5,故點B、D的坐標分別為(5,0)、(0,5),利用待定系數法即可求解;
(2)由題意可得M點坐標為(m,﹣m2+4m+5),則則P點坐標為(m,﹣m+5),表示出PM的長度:PM=-m2+4m+5-(-m+5)=-m2+5m=-(m-![]() )2+
)2+![]() ,利用二次函數的性質即可求解;
,利用二次函數的性質即可求解;
(3)過Q作QG∥y軸交BD于點G,交x軸于點E,作QH⊥BD于H,設出Q點坐標Q(x,﹣x2+4x+5),則G(x,﹣x+5),表示出QG的長度QG=|-x2+4x+5-(-x+5)|=|-x2+5x|,由條件可得△BOD是等腰直角三角形,,可證得△QHG為等腰直角三角形,則當△BDQ中BD邊上的高為3![]() 時,即QH=HG=3
時,即QH=HG=3![]() ,QG=
,QG=![]() ×3
×3![]() =6,|-x2+5x|=6,即可求解.
=6,|-x2+5x|=6,即可求解.
解:(1)y=﹣x+5,令x=0,則y=5,令y=0,則x=5,
故點B、D的坐標分別為(5,0)、(0,5),
則二次函數表達式為:y=﹣x2+bx+5,將點B坐標代入上式并解得:b=4,
故拋物線的表達式為:y=﹣x2+4x+5;
(2)設M點橫坐標為m(m>0),則P(m,﹣m+5),M(m,﹣m2+4m+5),
∴PM=﹣m2+4m+5﹣(﹣m+5)=﹣m2+5m=﹣(m-![]() )2+
)2+![]() ,
,
∴當m=![]() 時,PM有最大值
時,PM有最大值![]() ;
;
(3)如圖,過Q作QG∥y軸交BD于點G,交x軸于點E,作QH⊥BD于H,
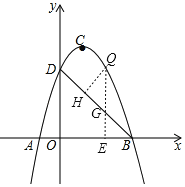
設Q(x,﹣x2+4x+5),則G(x,﹣x+5),
∴QG=|﹣x2+4x+5﹣(﹣x+5)|=|﹣x2+5x|,
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°,
∴△QHG是等腰直角三角形,
當△BDQ中BD邊上的高為3![]() 時,即QH=HG=3
時,即QH=HG=3![]() ,
,
∴QG=![]() ×3
×3![]() =6,
=6,
∴|﹣x2+5x|=6,
當﹣x2+5x=6時,解得x=2或x=3,
∴Q(2,9)或(3,8),
當﹣x2+5x=﹣6時,解得x=﹣1或x=6,
∴Q(﹣1,0)或(6,﹣7),
綜上可知存在滿足條件的點Q,其坐標為Q1(2,9),Q2(3,8),Q3(﹣1,0),Q4(6,﹣7).


科目:初中數學 來源: 題型:
【題目】如圖,已知一條直線過點(0,4),且與拋物線y=![]() x2交于A,B兩點,其中點A的橫坐標是-2.
x2交于A,B兩點,其中點A的橫坐標是-2.
(1)求這條直線的解析式及點B的坐標;
(2)在x軸上是否存在點C,使得△ABC是直角三角形?若存在,求出點C的坐標,若不存在,請說明理由;
(3)過線段AB上一點P,作PM∥x軸,交拋物線于點M,點M在第一象限,點N(0,1),當點M的橫坐標為何值時,MN+3MP的長度最大?最大值是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,一枚質地均勻的骰子,骰子有六個面并分別標有數字1,2,3,4,5,6.如圖2,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 7個圈,相鄰兩個圈間距相等.跳圈游戲的規則為:游戲者每擲一次骰子,骰子向上的一面上的數字是幾,就從圈
7個圈,相鄰兩個圈間距相等.跳圈游戲的規則為:游戲者每擲一次骰子,骰子向上的一面上的數字是幾,就從圈![]() 開始向前連續跳幾個間距.如:從圈
開始向前連續跳幾個間距.如:從圈![]() 起跳,第一次擲得3,就連續跳3個間距,跳到圈
起跳,第一次擲得3,就連續跳3個間距,跳到圈![]() ;若第二次擲得3,就從
;若第二次擲得3,就從![]() 開始連續跳3個間距,跳到圈
開始連續跳3個間距,跳到圈![]() ;若第二次擲得4,就從圈
;若第二次擲得4,就從圈![]() 開始連續跳4個間距,跳到圈
開始連續跳4個間距,跳到圈![]() 后返回到圈
后返回到圈![]() ;…設游戲者從圈
;…設游戲者從圈![]() 起跳.
起跳.
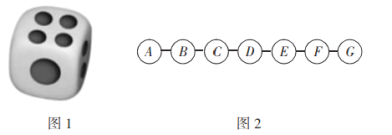
(1)小明隨機擲一次骰子,求跳到圈![]() 的概率
的概率![]() ;
;
(2)小亮隨機擲兩次骰子,用列表法或畫樹狀圖法求最后跳到圈![]() 的概率
的概率![]() ,并指出他與小明跳到圈
,并指出他與小明跳到圈![]() 的可能性一樣嗎?
的可能性一樣嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2 +bx+ 4與x軸的兩個交點分別為A(-4,0)、B(2,0),與y軸交于點C,頂點為D.E(1,2)為線段BC的中點,BC的垂直平分線與x軸、y軸分別交于F、G.
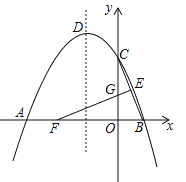
(1)求拋物線的函數解析式,并寫出頂點D的坐標;
(2)在直線EF上求一點H,使△CDH的周長最小,并求出最小周長;
(3)若點K在x軸上方的拋物線上運動,當K運動到什么位置時,
△EFK的面積最大?并求出最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
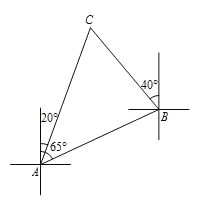
【題目】如圖,一艘船由A港沿北偏東65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏東20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏東20°方向.
求:(1)∠C的度數;
(2)A,C兩港之間的距離為多少km.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售一批名牌襯衫,平均每天可售出20件,每件盈利40元.為擴大銷售,增加盈利,商場決定采取適當的降價措施,經調查發現,如果每件襯衫每降價1元,商場平均每天可多售出2件.
(1)每件襯衫降價多少元時,商場平均每天的盈利是1050元?
(2)每件襯衫降價多少元時,商場平均每天盈利最大?最大盈利是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,一次函數![]() (a,b為常數,且
(a,b為常數,且![]() )與反比例函數
)與反比例函數![]() (m為常數,且
(m為常數,且![]() )的圖象交于點A(﹣2,1)、B(1,n).
)的圖象交于點A(﹣2,1)、B(1,n).

(1)求反比例函數和一次函數的解析式;
(2)連結OA、OB,求△AOB的面積;
(3)直接寫出當![]() 時,自變量x的取值范圍.
時,自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,如圖1,AB是⊙O的弦,點F是![]() 的中點,過點F作EF⊥AB于點E,易得點E是AB的中點,即AE=EB.⊙O上一點C(AC>BC),則折線ACB稱為⊙O的一條“折弦”.
的中點,過點F作EF⊥AB于點E,易得點E是AB的中點,即AE=EB.⊙O上一點C(AC>BC),則折線ACB稱為⊙O的一條“折弦”.
(1)當點C在弦AB的上方時(如圖2),過點F作EF⊥AC于點E,求證:點E是“折弦ACB”的中點,即AE=EC+CB.
(2)當點C在弦AB的下方時(如圖3),其他條件不變,則上述結論是否仍然成立?若成立說明理由;若不成立,那么AE、EC、CB滿足怎樣的數量關系?直接寫出,不必證明.
(3)如圖4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圓⊙O的半徑為2,過⊙O上一點P作PH⊥AC于點H,交AB于點M,當∠PAB=45°時,求AH的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
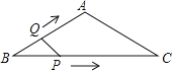
【題目】如圖,在等腰△ABC中,AB=AC=4cm,∠B=30°,點P從點B出發,以![]() cm/s的速度沿BC方向運動到點C停止,同時點Q從點B出發以2cm/s的速度沿B→A→C運動到點C停止.若△BPQ的面積為y運動時間為x(s),則下列圖象中能大致反映y與x之間關系的是( )
cm/s的速度沿BC方向運動到點C停止,同時點Q從點B出發以2cm/s的速度沿B→A→C運動到點C停止.若△BPQ的面積為y運動時間為x(s),則下列圖象中能大致反映y與x之間關系的是( )
A.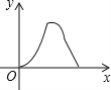 B.
B.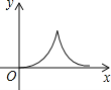 C.
C.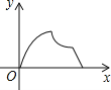 D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com