
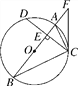
【題目】如圖,AB是⊙O的直徑,點C在⊙O上,CE AB于E, CD平分ECB, 交過點B的射線于D, 交AB于F, 且BC=BD.
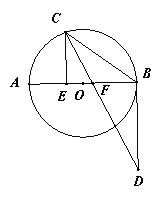
(1)求證:BD是⊙O的切線;
(2)若AE=9, CE=12, 求BF的長.
【答案】(1)證明見解析;(2)10.
【解析】
試題分析:(1)要證明BD是⊙O的切線,由已知條件轉化為證明∠DBA=90°即可;
(2)連接AC,利用三角形相似求出BE的值,由勾股定理求出BC的值,由已知條件再證明△EFC∽△BFD,相似三角形的性質利用:對應邊的比值相等即可求出BF的長.
試題解析:(1)證明:∵CE⊥AB,
∴∠CEB=90°.
∵CD平分∠ECB,BC=BD,
∴∠1=∠2,∠2=∠D.
∴∠1=∠D,
∴CE∥BD,
∴∠DBA=∠CEB=90°,
∵AB是⊙O的直徑,
∴BD是⊙O的切線;
(2)解:連接AC,
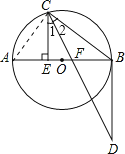
∵AB是⊙O直徑,
∴∠ACB=90°.
∵CE⊥AB,
∴∠AEC=∠BEC=90°,
∵∠A+∠ABC=90°,∠A+∠ACE=90°,
∴∠ACE=∠ABC,
∴△ACE∽△CBE,
∴![]() ,即CE2=AEEB,
,即CE2=AEEB,
∵AE=9,CE=12,
∴EB=16,
在Rt△CEB中,∠CEB=90,由勾股定理得 BC=20,
∴BD=BC=20,
∵∠1=∠D,∠EFC=∠BFD,
∴△EFC∽△BFD,
∴![]() ,
,
即![]()
∴BF=10.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,O是菱形ABCD的對角線AC,BD的交點,E,F分別是OA,OC的中點.下列結論:①S△ADE=S△EOD;②四邊形BFDE也是菱形;③△DEF是軸對稱圖形;④∠ADE=∠EDO;⑤四邊形ABCD面積為EF×BD.其中正確的結論有( )
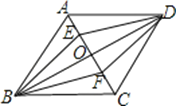
A. 5個 B. 4個 C. 3個 D. 2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩家超市以相同的價格出售同樣的商品,為了吸引顧客,各自推出不同的優惠方案;在甲超市累計購買商品超出200元之后,超出部分按原價8折優惠;在乙超市累計購買商品超出100元之后,超出部分按原價8.5折優惠,設顧客購物的原費用是x元(x>200).
(1)請用含x的代數式分別表示顧客在兩家超市購物所付的實際費用;
(2)李明慧準備購買300元的商品,你認為他應該去哪家超市?請說明理由;
(3)計算一下,李明慧購買多少元的商品時,到兩家超市購物所付的費用一樣?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料并解決問題:
(1)數學課上,老師提出如下問題:
觀察下列算式:
![]() ;
;
![]() ;
;
![]()
![]()
![]()
…
若字母![]() 表示自然數,用含
表示自然數,用含![]() 的式子表示觀察得到的規律是
的式子表示觀察得到的規律是![]() ;
;
(2)小云同學解決完老師提出的問題后,又繼續研究,發現:
①當![]() 表示負整數且
表示負整數且![]() 時,上述規律仍舊成立;
時,上述規律仍舊成立;
②當![]() 表示分數且
表示分數且![]() 時,上述規律仍舊成立.
時,上述規律仍舊成立.
請你對小云的兩個發現進行驗證,每個發現舉出一個算式;
(3)請你參照小云同學的研究思路,進行猜想,驗證、歸納,當![]() 時,
時,![]() (用含
(用含![]() 的代數式表示);
的代數式表示);
(4)進一步進行猜想、驗證、歸納,當![]() (
(![]() 為有理數)時,
為有理數)時,![]() (用含
(用含![]() ,
,![]() ,
,![]() 的代數式表示)。
的代數式表示)。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC,BD交于點O,AE⊥BC交CB延長線于E,CF∥AE交AD延長線于點F.
(1)求證:四邊形AECF是矩形;
(2)連接OE,若AE=4,AD=5,求OE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠按用戶的月需求量![]() (件)完成一種產品的生產,其中
(件)完成一種產品的生產,其中![]() .每件的售價為18萬元,每件的成本
.每件的售價為18萬元,每件的成本![]() (萬元)是基礎價與浮動價的和,其中基礎價保持不變,浮動價與月需求量
(萬元)是基礎價與浮動價的和,其中基礎價保持不變,浮動價與月需求量![]() (件)成反比.經市場調研發現,月需求量
(件)成反比.經市場調研發現,月需求量![]() 與月份
與月份![]() (
(![]() 為整數,
為整數,![]() )符合關系式
)符合關系式![]() (
(![]() 為常數),且得到了表中的數據.
為常數),且得到了表中的數據.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 與
與![]() 滿足的關系式,請說明一件產品的利潤能否是12萬元;
滿足的關系式,請說明一件產品的利潤能否是12萬元;
(2)求![]() ,并推斷是否存在某個月既無盈利也不虧損;
,并推斷是否存在某個月既無盈利也不虧損;
(3)在這一年12個月中,若第![]() 個月和第
個月和第![]() 個月的利潤相差最大,求
個月的利潤相差最大,求![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班數學科代表小芳對本年級同學參加課外興趣小組活動情況進行隨機抽樣調查,根據調查數據小芳同學還制作了參加課外興趣小組活動情況的兩個統計圖(見下圖)
(1)此次被調查的人數是多少?
(2)將圖②補充完整;
(3)求出圖①中表示“寫作”興趣小組的扇形圓心角度數;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形紙片ABCD的兩邊AB:BC=2:1,過點B折疊紙片,使點A落在邊CD上的點F處,折痕為BE.若AB的長為4,則EF的長為( )
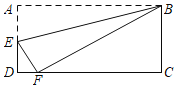
A. 8-4![]() B. 2
B. 2![]() C. 4
C. 4![]() 6D.
6D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,直徑AB⊥弦CD于點E,連接AC,BC,點F是BA延長線上的一點,且∠FCA=∠B.
(1)求證:CF是⊙O的切線;
(2)若AE=4,tan∠ACD=![]() ,求FC的長.
,求FC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com