
【題目】已知數軸上A,B兩點對應的數分別為a,b,且a,b滿足|a+20|=﹣(b﹣13)2,點C對應的數為16,點D對應的數為﹣13.
(1)求a,b的值;
(2)點A,B沿數軸同時出發相向勻速運動,點A的速度為6個單位/秒,點B的速度為2個單位/秒,若t秒時點A到原點的距離和點B到原點的距離相等,求t的值;
(3)在(2)的條件下,點A,B從起始位置同時出發.當A點運動到點C時,迅速以原來的速度返回,到達出發點后,又折返向點C運動.B點運動至D點后停止運動,當B停止運動時點A也停止運動.求在此過程中,A,B兩點同時到達的點在數軸上對應的數.
【答案】(1)a=﹣20,c=13;(2)t的值為![]() s或
s或 ![]() s.(3)
s.(3)![]() ,﹣
,﹣![]() .
.
【解析】試題分析:(1)根據非負數的性質,建立方程求出a,b的值;
(2)根據A,B兩點到原點O的距離相等分兩種情況,當A、B在原點的右側A、B相遇和A、B在原點的異側時,建立方程求出其解即可;
(3)分三種情況討論:當A、B在原點的右側相遇時;當點A從點C返回出發點時與B相遇;當點A從出發點返回點C時與點B相遇.分別依據線段的和差關系列方程求解即可.
試題解析:解:(1)由題意得:|a+20|+(b﹣13)2=0,∴a+20=0,b﹣13=0,解得:a=﹣20,c=13;
(2)∵點B對應的數為13,A對應的數是﹣20,∴AB=36,AO=20,BO=13.
當A、B在原點的異側時,若點A到原點的距離和點B到原點的距離相等,則
20﹣6t=13﹣2t,解得:t=![]() .
.
當A、B在原點的右側相遇時,點A到原點的距離和點B到原點的距離相等,則
6t+2t=33,t=![]() ,∴A,B兩點到原點O的距離相等時,t的值為
,∴A,B兩點到原點O的距離相等時,t的值為![]() s或
s或 ![]() s.
s.
(3)B點運動至D點所需的時間為26÷2=13(s),故t≤13.
由(2)得,當t=![]() 時,A,B兩點同時到達的點表示的數是13﹣
時,A,B兩點同時到達的點表示的數是13﹣![]() ×2=
×2=![]() ;
;
由題意得:當點A從點C返回出發點時,若與B相遇,則
6t﹣2t=20+16+(16﹣13),解得:t=![]() ,此時A,B兩點同時到達的點表示的數是13﹣
,此時A,B兩點同時到達的點表示的數是13﹣![]() ×2=﹣
×2=﹣![]() .
.
當點A從出發點返回點C時,若與點B相遇,則
6t+2t=2(20+16)+20+13,解得t=13![]() (不合題意);
(不合題意);
綜上所述:A,B兩點同時到達的點在數軸上表示的數為: ![]() ,﹣
,﹣![]() .
.


科目:初中數學 來源: 題型:
【題目】18世紀最杰出的瑞士數學家歐拉,最先把關于x的多項式用符號“f(x)”表示,如f(x)=﹣3x2+2x﹣1,把x=﹣2時多項式的值表示為f(﹣2),則f(﹣2)=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從去年發生非洲豬瘟以來,各地豬肉緊缺,價格一再飆升,為平穩肉價,某物流公司受命將300噸豬肉運往某地,現有A,B兩種型號的車共19輛可供調用,已知A型車每輛可裝20噸,B型車每輛可裝15噸.在不超載的條件下,19輛車恰好把300噸豬肉一次運完,則需A,B型車各多少輛?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 經過B(﹣1,0),D(﹣2,5)兩點,與x軸另一交點為A,點H是線段AB上一動點,過點H的直線PQ⊥x軸,分別交直線AD、拋物線于點Q,P.
經過B(﹣1,0),D(﹣2,5)兩點,與x軸另一交點為A,點H是線段AB上一動點,過點H的直線PQ⊥x軸,分別交直線AD、拋物線于點Q,P.
(1)求拋物線的解析式;
(2)是否存在點P,使∠APB=90°,若存在,求出點P的橫坐標,若不存在,說明理由;
(3)連接BQ,一動點M從點B出發,沿線段BQ以每秒1個單位的速度運動到Q,再沿線段QD以每秒![]() 個單位的速度運動到D后停止,當點Q的坐標是多少時,點M在整個運動過程中用時t最少?
個單位的速度運動到D后停止,當點Q的坐標是多少時,點M在整個運動過程中用時t最少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一條筆直的公路上有![]() 、
、![]() 兩地,甲從
兩地,甲從![]() 地去
地去![]() 地,乙從
地,乙從![]() 地去
地去![]() 地然后立即原路返回
地然后立即原路返回![]() 地,返回時的速度是原來的2倍,如圖是甲、乙兩人離
地,返回時的速度是原來的2倍,如圖是甲、乙兩人離![]() 地的距離
地的距離![]() (千米)和時間
(千米)和時間![]() (小時)之間的函數圖象.
(小時)之間的函數圖象.
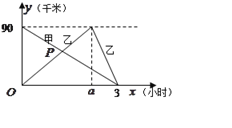
請根據圖象回答下列問題:
(1)![]() 、
、![]() 兩地的距離是 千米,
兩地的距離是 千米, ![]() ;
;
(2)求![]() 的坐標,并解釋它的實際意義;
的坐標,并解釋它的實際意義;
(3)請直接寫出當![]() 取何值時,甲乙兩人相距15千米.
取何值時,甲乙兩人相距15千米.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com