
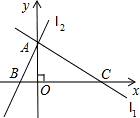
 如圖,直線L1交直線L2于y軸上一點A(0,6),交x軸上另一點C.l2交x軸于另一點B,二次函數y=ax2-6ax-16a (a>0)的圖象過B、C兩點,點P是線段OC上由O向C移動的動點,線段OP=t(1<t<8)
如圖,直線L1交直線L2于y軸上一點A(0,6),交x軸上另一點C.l2交x軸于另一點B,二次函數y=ax2-6ax-16a (a>0)的圖象過B、C兩點,點P是線段OC上由O向C移動的動點,線段OP=t(1<t<8)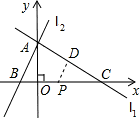 解:(1)拋物線的解析式中,當y=0時,0=a(x2-6x-16),解得:x1=-2,x2=8;
解:(1)拋物線的解析式中,當y=0時,0=a(x2-6x-16),解得:x1=-2,x2=8;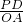 =
= ,即
,即 =
=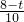
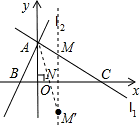 (2)由(1)知:拋物線的對稱軸 x=3;
(2)由(1)知:拋物線的對稱軸 x=3; x+6,則 M(3,
x+6,則 M(3, ).
). );
); ,k=-
,k=-
 x+6
x+6 ;即 N(
;即 N( ,0).
,0).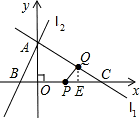 (3)過Q作QE⊥x軸于點E,則 QE=
(3)過Q作QE⊥x軸于點E,則 QE= QE=
QE= t,CE=
t,CE= QC=
QC= t,OE=OC-CE=8-
t,OE=OC-CE=8- t;
t; t,
t, t).
t). PC•QE=
PC•QE= ×(8-t)×
×(8-t)× t=-
t=- t2+
t2+ t(1<t<8).
t(1<t<8). t-t)2+(
t-t)2+( t)2=
t)2= t2-
t2-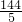 t+64,PC2=(8-t)2=t2-16t+64,CQ2=t2;
t+64,PC2=(8-t)2=t2-16t+64,CQ2=t2; t2-
t2-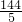 t+64=t2-16t+64,解得:t1=0(舍去),t2=
t+64=t2-16t+64,解得:t1=0(舍去),t2=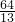 ;
; t2-
t2-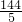 t+64=t2,解得:t1=8(舍去),t2=
t+64=t2,解得:t1=8(舍去),t2=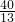 ;
;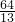 、t2=
、t2= 、t3=4.
、t3=4.

科目:初中數學 來源: 題型:
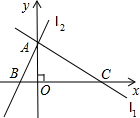 (2012•荊州模擬)如圖,直線L1交直線L2于y軸上一點A(0,6),交x軸上另一點C.l2交x軸于另一點B,二次函數y=ax2-6ax-16a (a>0)的圖象過B、C兩點,點P是線段OC上由O向C移動的動點,線段OP=t(1<t<8)
(2012•荊州模擬)如圖,直線L1交直線L2于y軸上一點A(0,6),交x軸上另一點C.l2交x軸于另一點B,二次函數y=ax2-6ax-16a (a>0)的圖象過B、C兩點,點P是線段OC上由O向C移動的動點,線段OP=t(1<t<8)查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
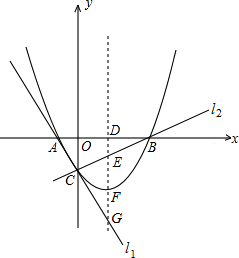 ,拋物線y=ax2+bx+c(a≠0)經過A、B、C三點.
,拋物線y=ax2+bx+c(a≠0)經過A、B、C三點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
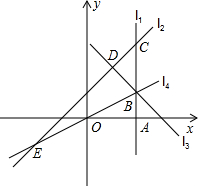 如圖,直線l1⊥x軸于點A(2,0),點B是直線l1上的動點.直線l2:y=x+1交l1于點C,過點B作直線l3垂直于l2,垂足為D,過點O,B的直線l4交l2于點E,當直線l1,l2,l3能圍成三角形時,設該三角形面積為S1,當直線l2,l3,l4能圍成三角形時,設該三角形面積為S2.
如圖,直線l1⊥x軸于點A(2,0),點B是直線l1上的動點.直線l2:y=x+1交l1于點C,過點B作直線l3垂直于l2,垂足為D,過點O,B的直線l4交l2于點E,當直線l1,l2,l3能圍成三角形時,設該三角形面積為S1,當直線l2,l3,l4能圍成三角形時,設該三角形面積為S2. S1,則∠BOA的度數為______.
S1,則∠BOA的度數為______.查看答案和解析>>
科目:初中數學 來源:2012年湖北省荊州市中考數學調研試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com