Question

（2013•內江）已知二次函數y=ax²+bx+c（a＞0）的圖象與x軸交于A（x₁，0）、B（x₂，0）（x₁＜x₂）兩點，與y軸交于點C，x₁，x₂是方程x²+4x-5=0的兩根．
（1）若拋物線的頂點為D，求S_△ABC：S_△ACD的值；
（2）若∠ADC=90°，求二次函數的解析式．

Answer 1

分析：（1）首先解一元二次方程，求出點A、點B的坐標，得到含有字母a的拋物線的交點式；然后分別用含字母a的代數式表示出△ABC與△ACD的面積，最后得出結論；
（2）在Rt△ACD中，利用勾股定理，列出一元二次方程，求出未知系數a，得出拋物線的解析式．

解答：解：（1）解方程x²+4x-5=0，得x=-5或x=1，
由于x₁＜x₂，則有x₁=-5，x₂=1，∴A（-5，0），B（1，0）．
拋物線的解析式為：y=a（x+5）（x-1）（a＞0），
∴對稱軸為直線x=-2，頂點D的坐標為（-2，-9a），
令x=0，得y=-5a，
∴C點的坐標為（0，-5a）．
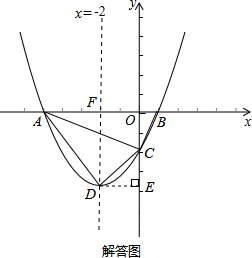
依題意畫出圖形，如右圖所示，則OA=5，OB=1，AB=6，OC=5a，
過點D作DE⊥y軸于點E，則DE=2，OE=9a，CE=OE-OC=4a．
S_△ACD=S_梯形ADEO-S_△CDE-S_△AOC
=

1

2

（DE+OA）•OE-

1

2

DE•CE-

1

2

OA•OC
=

1

2

（2+5）•9a-

1

2

×2×4a-

1

2

×5×5a
=15a，
而S_△ABC=

1

2

AB•OC=

1

2

×6×5a=15a，
∴S_△ABC：S_△ACD=15a：15a=1：1；

（2）如解答圖，過點D作DE⊥y軸于E
在Rt△DCE中，由勾股定理得：CD²=DE²+CE²=4+16a²，
在Rt△AOC中，由勾股定理得：AC²=OA²+OC²=25+25a²，
設對稱軸x=-2與x軸交于點F，則AF=3，
在Rt△ADF中，由勾股定理得：AD²=AF²+DF²=9+81a²．
∵∠ADC=90°，∴△ACD為直角三角形，
由勾股定理得：AD²+CD²=AC²，
即（9+81a²）+（4+16a²）=25+25a²，化簡得：a²=

1

6

，
∵a＞0，
∴a=

6

6

，
∴拋物線的解析式為：y=

6

6

（x+5）（x-1）=

6

6

x²+

2 6

3

x-

5 6

6

．

點評：本題考查了二次函數的圖象與性質、一元二次方程的解法、直角三角形與勾股定理、幾何圖形面積的計算等知識點，難度不是很大，但涉及的計算較多，需要仔細認真，避免出錯．注意第（1）問中求△ACD面積的方法．