
| DF |
| BE |
| AD |
| AB |
| DF |
| 12 |
| 12-4 |
| 12 |
| GF2+GE2 |
| 42+42 |
| 2 |
| 2 |
| 2 |
| 2 |



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
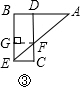
 24����D����֪��AD�ǡ�ABC��BC߅���о����tS��ABD=S��ACD������(j��)��
24����D����֪��AD�ǡ�ABC��BC߅���о����tS��ABD=S��ACD������(j��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
 ��2013•�ӱ�һģ����D1���ھ���ABCD�У����cP���cB���l(f��)����BC��CD�\�����cDֹͣ���O(sh��)�cP�\�ӵ�·�̞�x����ABP����e��y��y�P(gu��n)��x�ĺ���(sh��)�D����D2��ʾ���t��ABC����e�ǣ�������
��2013•�ӱ�һģ����D1���ھ���ABCD�У����cP���cB���l(f��)����BC��CD�\�����cDֹͣ���O(sh��)�cP�\�ӵ�·�̞�x����ABP����e��y��y�P(gu��n)��x�ĺ���(sh��)�D����D2��ʾ���t��ABC����e�ǣ��������鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
| 1 | 2 |
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com