
 x2+mx+n的圖象經過A,C兩點.
x2+mx+n的圖象經過A,C兩點. +1)倍?若存在,請直接寫出點P的坐標;若不存在,請說明理由.
+1)倍?若存在,請直接寫出點P的坐標;若不存在,請說明理由.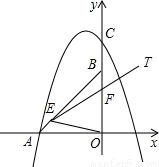
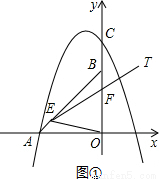 解:(1)如圖①,∵A(-2,0)B(0,2)
解:(1)如圖①,∵A(-2,0)B(0,2)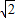 ,
,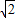 ,即C(0,2
,即C(0,2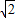 )
)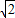 x2+mx+n的圖象經過A、C兩點
x2+mx+n的圖象經過A、C兩點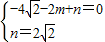 ,
,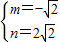 .
.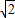 x2-
x2-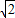 x+2
x+2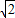 .
.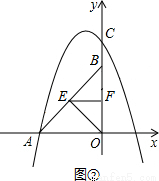
 OB=
OB= ×2=1
×2=1 
 =
=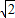
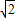 ∴E(-
∴E(-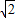 ,2-
,2-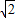 )
) ,2-
,2-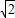 ).
).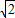 ,2-
,2-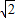 ).
).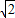 .
.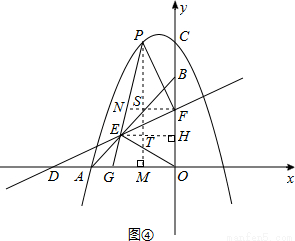 由OE=EF,易知點E為Rt△DOF斜邊上的中點,即DE=EF,
由OE=EF,易知點E為Rt△DOF斜邊上的中點,即DE=EF,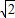 +1)S△EDG=(2
+1)S△EDG=(2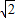 +1)S△EFN,
+1)S△EFN,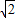 +1):1.
+1):1.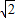 .
.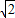 +1,
+1,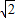 +1)•ST=(2
+1)•ST=(2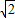 +1)(2-
+1)(2-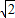 )=3
)=3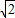 -2;
-2;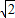 ,即點P的縱坐標為2
,即點P的縱坐標為2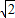 ,
,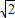 x2-
x2-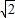 x+2
x+2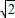 =2
=2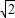 ,
,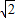 )或(-1,2
)或(-1,2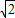 ).
). +1)倍;
+1)倍;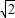 )或(-1,2
)或(-1,2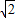 ).
).

 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:
 如圖,在平面直角坐標系中,直y=
如圖,在平面直角坐標系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在平面直角坐標系中,原點O處有一乒乓球發射器向空中發射乒乓球,乒乓球飛行路線是一條拋物線,在地面上落點落在X軸上為點B.有人在線段OB上點C(靠點B一側)豎直向上擺放無蓋的圓柱形桶,試圖讓乒乓球落入桶內.已知OB=4米,OC=3米,乒乓球飛行最大高度MN=5米,圓柱形桶的直徑為0.5,高為0.3米(乒乓球的體積和圓柱形桶的厚度忽略不計).
如圖,在平面直角坐標系中,原點O處有一乒乓球發射器向空中發射乒乓球,乒乓球飛行路線是一條拋物線,在地面上落點落在X軸上為點B.有人在線段OB上點C(靠點B一側)豎直向上擺放無蓋的圓柱形桶,試圖讓乒乓球落入桶內.已知OB=4米,OC=3米,乒乓球飛行最大高度MN=5米,圓柱形桶的直徑為0.5,高為0.3米(乒乓球的體積和圓柱形桶的厚度忽略不計).查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 3 |

查看答案和解析>>
科目:初中數學 來源:2012屆重慶萬州區巖口復興學校九年級下第一次月考數學試卷(帶解析) 題型:解答題
已知:直角梯形AOBC在平面直角坐標系中的位置如圖,若AC∥OB,OC平分∠AOB,CB⊥x軸于B,點A坐標為(3 ,4). 點P從原點O開始以2個單位/秒速度沿x軸正向運動 ;同時,一條平行于x軸的直線從AC開始以1個單位/秒速度豎直向下運動 ,交OA于點D,交OC于點M,交BC于點E. 當點P到達點B時,直線也隨即停止運動. 
(1)求出點C的坐標;
(2)在這一運動過程中, 四邊形OPEM是什么四邊形?請說明理由。若
用y表示四邊形OPEM的面積 ,直接寫出y關于t的函數關系式及t的
范圍;并求出當四邊形OPEM的面積y的最大值?
(3)在整個運動過程中,是否存在某個t值,使⊿MPB為等腰三角形?
若有,請求出所有滿足要求的t值.
查看答案和解析>>
科目:初中數學 來源:2013年浙江省湖州市中考數學模擬試卷(十一)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com