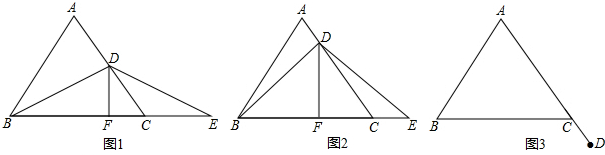
(1)證明:如圖1,
①∵△ABC為等邊三角形,
∴∠ABC=∠ACB=60°,
∵CD=CE,
∴∠E=∠CDE,
而∠DCB=∠E+∠CDE=60°,
∴∠E=30゜,
∵DA=DC,
∴∠DAC=

∠ABC=30°,
∴DB=DE;
②∵DF⊥BC,
∴BF=EF;
2)BF=EF仍然成立.理由如下:
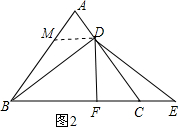
作DM∥BC交AB于M,如圖2,
∵△ABC為等邊三角形,
∴∠A=∠ABC=∠ACB=60°,AB=AC,
∴∠DCE=120°,
∵DM∥BC,
∴∠AMD=60°,
∴∠BMD=60°,△AMD為等邊三角形,
∴AD=DM=AM,
∵AD=CE,
∴DM=EC,
∴AB-AM=AC-AD,
∴MB=DC,
∴△BMD≌△DCE(SAS),
∴BD=DE,
而DF⊥BC,
∴BF=EF;
(3)(2)中的結論仍然成立.理由如下:
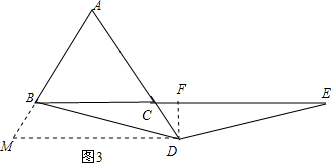
如圖3,作DM∥BC交AB的延長線于M,
易證△AMD為等邊三角形,
∴AM=AD=MD,∠M=60°,
而AB=AC,
∴BM=CD,
∵AD=CE,
∴MD=CE,
∵∠ECD=∠ACB=60°,
∴∠M=∠ECD,
∴△BMD≌△DCE(SAS),
∴BD=DE,
而DF⊥BC,
BF=EF.
分析:(1)根據等邊三角形的性質得∠ABC=∠ACB=60°,由CD=CE得∠E=∠CDE,再利用∠DCB=∠E+∠CDE=60°得到∠E=30゜,由DA=DC,根據等腰三角形性質得∠DAC=

∠ABC=30°,根據等腰三角形的判定得DB=DE;然后根據等腰三角形的性質由DF⊥BC得到BF=EF;
(2)作DM∥BC交AB于M,根據等邊三角形的性質得∠A=∠ABC=∠ACB=60°,AB=AC,則∠DCE=120°,由DM∥BC得∠AMD=60°,易得△AMD為等邊三角形,則AD=DM=AM,而AD=CE,則DM=EC,所以MB=DC,利用“SAS”可判斷△BMD≌△DCE,則BD=DE,然后根據等腰三角形的性質由DF⊥BC得到BF=EF;
(3)作DM∥BC交AB的延長線于M,易證△AMD為等邊三角形,則AM=AD=MD,∠M=60°,可得到BM=CD,而AD=CE,所以MD=CE,加上∠M=∠ECD=60°,
于是可根據“SAS”判斷△BMD≌△DCE,則BD=DE,然后根據等腰三角形的性質由DF⊥BC得到BF=EF.
點評:本題考查了等邊三角形的性質:等邊三角形的三個內角都相等,且都等于60°.也考查了等腰三角形的性質以及三角形全等的判定與性質.



 ∠ABC=30°,
∠ABC=30°, ∠ABC=30°,根據等腰三角形的判定得DB=DE;然后根據等腰三角形的性質由DF⊥BC得到BF=EF;
∠ABC=30°,根據等腰三角形的判定得DB=DE;然后根據等腰三角形的性質由DF⊥BC得到BF=EF;

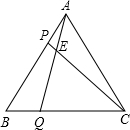 重合),且AP=BQ,AQ、CP相交于點E.
重合),且AP=BQ,AQ、CP相交于點E.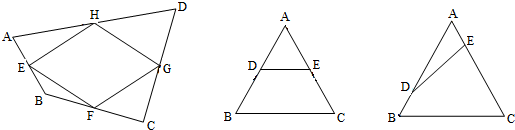
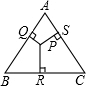 如圖,等邊三角形ABC內有一點P,過點P向三邊作垂線,垂足分別為S、Q、R,且PQ=6,PR=8,PS=10,則△ABC的面積等于( )
如圖,等邊三角形ABC內有一點P,過點P向三邊作垂線,垂足分別為S、Q、R,且PQ=6,PR=8,PS=10,則△ABC的面積等于( )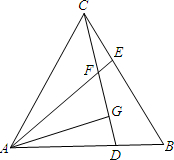 如圖,等邊三角形ABC中,D、E分別在AB、BC邊上,且AD=BE,AE與CD交于點F,AG⊥CD于點G.下列結論:①AE=CD;②∠AFC=120°;③△ADF是正三角形;④
如圖,等邊三角形ABC中,D、E分別在AB、BC邊上,且AD=BE,AE與CD交于點F,AG⊥CD于點G.下列結論:①AE=CD;②∠AFC=120°;③△ADF是正三角形;④