
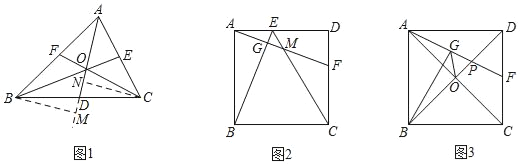
【題目】(探索發現)如圖1,△ABC中,點D,E,F分別在邊BC,AC,AB上,且AD,BE,CF相交于同一點O.用”S”表示三角形的面積,有S△ABD:S△ACD=BD:CD,這一結論可通過以下推理得到:過點B作BM⊥AD,交AD延長線于點M,過點C作CN⊥AD于點N,可得S△ABD:S△ACD=![]() ,又可證△BDM~△CDN,∴BM:CN=BD:CD,∴S△ABD:S△ACD=BD:CD.由此可得S△BAO:S△BCO= ;S△CAO:S△CBO= ;若D,E,F分別是BC,AC,AB的中點,則S△BFO:S△ABC= .
,又可證△BDM~△CDN,∴BM:CN=BD:CD,∴S△ABD:S△ACD=BD:CD.由此可得S△BAO:S△BCO= ;S△CAO:S△CBO= ;若D,E,F分別是BC,AC,AB的中點,則S△BFO:S△ABC= .
(靈活運用)如圖2,正方形ABCD中,點E,F分別在邊AD,CD上,連接AF,BE和CE,AF分別交BE,CE于點G,M.
(1)若AE=DF.判斷AF與BE的位置關系與數量關系,并說明理由;
(2)若點E,F分別是邊AD,CD的中點,且AB=4.則四邊形EMFD的面積是 .
(拓展應用)如圖3,正方形ABCD中,AB=4,對角線AC,BD相交于點O.點F是邊CD的中點.AF與BD相交于點P,BG⊥AF于點G,連接OG,請直接寫出S△OGP的值.
【答案】[探索發現] AE:EC,AF:BF,1:6.[靈活運用](1)結論:AF=BE,AF⊥BE.(2)![]() ;[拓展應用] S△GOP=
;[拓展應用] S△GOP=![]() .
.
【解析】
【探索發現】利用等高模型,解決問題即可.
【靈活運用】
(1)結論:AF=BE,AF⊥BE.證明△BAE≌△ADF(SAS)即可解決問題.
(2)根據對稱性可知△DME,△DMF,關于直線DM對稱,推出S△DME=S△DMF,由AE=DE,推出S△AEM=S△DME=S△DMF,求出△ADF的面積即可解決問題.
【拓展應用】
由△GPO∽△BPA,推出![]() 即可解決問題.
即可解決問題.
解:探索發現:由題意:S△BAO:S△BCO=AE:EC;S△CAO:S△CBO=AF:BF;若D,E,F分別是BC,AC,AB的中點,則S△BFO:S△ABC=1:6,
故答案為:AE:EC,AF:BF,1:6.
靈活運用:(1)結論:AF=BE,AF⊥BE.
理由:如圖2中,
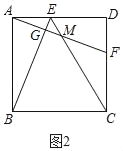
∵四邊形ABCD是正方形,
∴AB=AD,∠BAE=∠ADF=90°,
∵AE=DF,
∴△BAE≌△ADF(SAS),
∴BE=AF,∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AGE=90°,
∴AF⊥BE.
(2)如圖2﹣1中,連接DM.
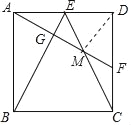
根據對稱性可知△DME,△DMF,關于直線DM對稱,
∴S△DME=S△DMF,
∵AE=DE,
∴S△AEM=S△DME=S△DMF,
∵S△ADF=![]() ×4×2=4,
×4×2=4,
∴S△AEM=S△DME=S△DMF=![]() ,
,
∴S四邊形EMFD=![]() .
.
故答案為![]() .
.
拓展應用:如圖3中,
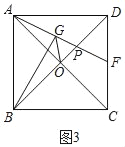
∵四邊形ABCD是正方形,
∴AB=BC=CD=AD=4,AC=BD=4![]() ,OA=OB=OD=OC=2
,OA=OB=OD=OC=2![]() ,
,
∵DF=FC,
∴DF=FC=2,
∵DF∥AB,
∴![]() ,
,
∴OP:OB=OP:OA=1:3,
∵BG⊥PA,AO⊥OB,
∴∠AGB=∠AOB=90°,
∵∠OAP+∠APO=90°,∠PBG+∠BPG=90°,
∴∠PAO=∠PBG,
∵∠APO=∠BPG,
∴△AOP∽△BGP,
∴![]()
∴![]() ,∵∠GPO=∠BPA,
,∵∠GPO=∠BPA,
∴△GPO∽△BPA,
∴![]() ,
,
∴S△ABP=![]() S△ABD=
S△ABD=![]() ,
,
∴S△GOP=![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】為改善教學條件,學校準備對現有多媒體設備進行升級改造,已知購買3個鍵盤和1個鼠標需要190元;購買2個鍵盤和3個鼠標需要220元;
(1)求鍵盤和鼠標的單價各是多少元?
(2)經過與經銷商洽談,鍵盤打八折,鼠標打八五折.若學校計劃購買鍵盤和鼠標共50件,且總費用不超過1820元,則最多可購買鍵盤多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
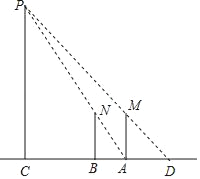
【題目】甲和乙兩位同學想測量一下廣場中央的照明燈P的高度,如圖,當甲站在A處時,乙測得甲的影子長AD正好與他的身高AM相等,接著甲沿AC方向繼續向前走,走到點B處時,甲的影子剛好是線段AB,此時測得AB的長為1.2m.已知甲直立時的身高為1.8m,求照明燈的高CP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BC>AB>AC.甲、乙兩人想在BC上取一點P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂線,交BC于P點,則P即為所求;
(乙)以B為圓心,AB長為半徑畫弧,交BC于P點,則P即為所求.
對于兩人的作法,下列判斷何者正確?( )
![]()
A. 兩人皆正確B. 兩人皆錯誤C. 甲正確,乙錯誤D. 甲錯誤,乙正確
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某賓館有若干間住房,住宿記錄提供了如下信息:
(1)4月17日全部住滿,一天住宿費收入為12000元;
(2)4月18日有20間房空著,一天住宿費收入為9600元;
(3)該賓館每間房每天收費標準相同.
①一個分式方程,求解該賓館共有多少間住房,每間住房每天收費多少元?
②通過市場調查發現,每間住房每天的定價每增加10元,就會有5個房間空閑;已知該賓館空閑房間每天每間支出費用10元,有顧客居住房間每天每間支出費用20元,問房價定為多少元時,該賓館一天的利潤為11000元?(利潤=住宿費收入﹣支出費用)
③在(2)的計算基礎上,你能發現房價定為多少元時,該賓館一天的利潤最大?請直接寫出結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D為⊙O上一點,點C在直線BA的延長線上,且∠CDA=∠CBD.

(1)求證:CD是⊙O的切線;
(2)若BC=8cm,tan∠CDA=![]() ,求⊙O的半徑;
,求⊙O的半徑;
(3)在(2)條件下,過點B作⊙O的切線交CD的延長線于點E,連接OE,求四邊形OEDA的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,CD是⊙O的一條弦,且CD⊥AB于點E,連接AD,BC,CO
(1)當∠BCO=25°時,求∠A的度數;
(2)若CD=4![]() ,BE=4,求⊙O的半徑.
,BE=4,求⊙O的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、D、C、F在同一條直線上,AD=CF,AB=DE,BC=EF.
(1)求證:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】菱形ABCD中、∠BAD=120°,點O為射線CA 上的動點,作射線OM與直線BC相交于點E,將射線OM繞點O逆時針旋轉60°,得到射線ON,射線ON與直線CD相交于點F.
(1)如圖①,點O與點A重合時,點E,F分別在線段BC,CD上,請直接寫出CE,CF,CA三條段段之間的數量關系;
(2)如圖②,點O在CA的延長線上,且OA=![]() AC,E,F分別在線段BC的延長線和線段CD的延長線上,請寫出CE,CF,CA三條線段之間的數量關系,并說明理由;
AC,E,F分別在線段BC的延長線和線段CD的延長線上,請寫出CE,CF,CA三條線段之間的數量關系,并說明理由;
(3)點O在線段AC上,若AB=6,BO=2![]() ,當CF=1時,請直接寫出BE的長.
,當CF=1時,請直接寫出BE的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com