
 體入住一律五折優惠.一個50人的旅游團在十月二號到該酒店住宿,租住了一些三人間,雙人間客房.
體入住一律五折優惠.一個50人的旅游團在十月二號到該酒店住宿,租住了一些三人間,雙人間客房.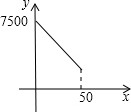 解:(1)設三人間有a間,雙人間有b間.根據題意得
解:(1)設三人間有a間,雙人間有b間.根據題意得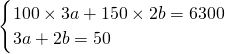 .
.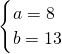 .
. 、
、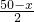 為整數值的增大值時,即x=48時,住宿費用最低.
為整數值的增大值時,即x=48時,住宿費用最低.

 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:初中數學 來源: 題型:
 體入住一律五折優惠.一個50人的旅游團在十月二號到該酒店住宿,租住了一些三人間,雙人間客房.
體入住一律五折優惠.一個50人的旅游團在十月二號到該酒店住宿,租住了一些三人間,雙人間客房.查看答案和解析>>
科目:初中數學 來源:廣東省期末題 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com