
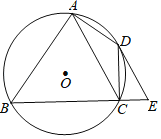
【題目】如圖,四邊形ABCD內接于⊙O,∠BAD=90°,點E在BC的延長線上,且∠DEC=∠BAC.
(1)求證:DE是⊙O的切線;
(2)若AC∥DE,當AB=8,CE=2時,求AC的長.
【答案】(1)證明見解析;(2)AC的長為![]() .
.
【解析】(1)先判斷出BD是圓O的直徑,再判斷出BD⊥DE,即可得出結論;
(2)先判斷出AC⊥BD,進而求出BC=AB=8,進而判斷出△BCD∽△DCE,求出CD,再用勾股定理求出BD,最后判斷出△CFD∽△BCD,即可得出結論.
(1)如圖,連接BD,

∵∠BAD=90°,
∴點O必在BD上,即:BD是直徑,
∴∠BCD=90°,
∴∠DEC+∠CDE=90°.
∵∠DEC=∠BAC,
∴∠BAC+∠CDE=90°.
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,
∴∠BDE=90°,即:BD⊥DE.
∵點D在⊙O上,
∴DE是⊙O的切線;
(2)∵DE∥AC.
∵∠BDE=90°,
∴∠BFC=90°,
∴CB=AB=8,AF=CF=![]() AC,
AC,
∵∠CDE+∠BDC=90°,∠BDC+∠CBD=90°,
∴∠CDE=∠CBD.
∵∠DCE=∠BCD=90°,
∴△BCD∽△DCE,
∴![]() ,
,
∴![]() ,
,
∴CD=4.
在Rt△BCD中,BD=![]() =4
=4![]() ,
,
同理:△CFD∽△BCD,
∴![]() ,
,
∴![]() ,
,
∴CF=![]() ,
,
∴AC=2AF=![]() .
.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:
【題目】某經銷商銷售一種產品,這種產品的成本價為10元/千克,市場調查發現,該產品每天的銷售量y(千克)與銷售價x(元/千克,且10≤x≤18)之間的函數關系如圖所示:

(1)求y(千克)與銷售價z的函數關系式;
(2)該經銷商想要每天獲得150元的銷售利潤,銷售價應定為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
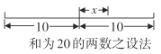
【題目】公元3世紀,古希臘數學家丟番圖(Diophantus)在其《算術》一書中設置了以下問題:已知兩正整數之和為20,乘積為96,求這兩個數.因為兩數之和為20,所以這兩個數不可能同時大于10,也不可能同時小于10,必定是一個大于10,一個小于10.根據如圖所示的設法,可設一個數為![]() ,則另一個數為
,則另一個數為![]() ,根據兩數之積為96,可得
,根據兩數之積為96,可得![]() .請根據以上思路解決下列問題:
.請根據以上思路解決下列問題:
(1)若兩個正整數之和為100,大數比小數大![]() ,根據丟番圖的設法,這兩個正整數可表示為____和___;
,根據丟番圖的設法,這兩個正整數可表示為____和___;
(2)請你根據丟番圖的運算方法,計算![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列事件中,發生的概率是![]() 的是( )
的是( )
A.從一副撲克牌中,任意抽取其中的一張,抽到紅桃的概率
B.一個圓盤被染成紅、黃、藍、紫四種顏色,隨機轉動一次,轉盤停止時,指針剛好指向紅色的概率
C.小明開車到十字路口時,遇到紅燈的概率
D.一道單選題有![]() 四個備用選項, 從中隨機選一個作答,答對的概率
四個備用選項, 從中隨機選一個作答,答對的概率
查看答案和解析>>
科目:初中數學 來源: 題型:
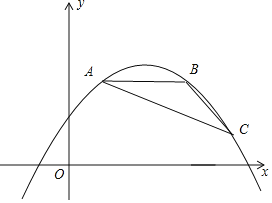
【題目】如圖,點A,B,C都在拋物線y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x軸,∠ABC=135°,且AB=4.
<a<0)上,AB∥x軸,∠ABC=135°,且AB=4.
(1)填空:拋物線的頂點坐標為 (用含m的代數式表示);
(2)求△ABC的面積(用含a的代數式表示);
(3)若△ABC的面積為2,當2m﹣5≤x≤2m﹣2時,y的最大值為2,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,AD=3,矩形內部有一動點P滿足S△PAB=![]() S矩形ABCD,則點P到A、B兩點的距離之和PA+PB的最小值為______.
S矩形ABCD,則點P到A、B兩點的距離之和PA+PB的最小值為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com