
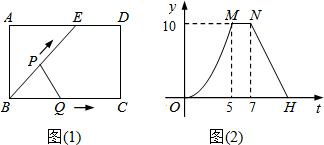
如圖1,點E為矩形ABCD邊AD上一點,點P,點Q同時從點B出發,點P沿BE→ED→DC 運動![]() 到點C停止,點Q沿BC運動到點C停止,它們運動的速度都是1cm/s,設P,Q出發t秒時,△BPQ的面積為ycm,已知y與t的函數關系的圖形如圖2(曲線OM為拋物線的一部分),則下列結論:①AD=BE=5cm;②當0<t≤5時,
到點C停止,點Q沿BC運動到點C停止,它們運動的速度都是1cm/s,設P,Q出發t秒時,△BPQ的面積為ycm,已知y與t的函數關系的圖形如圖2(曲線OM為拋物線的一部分),則下列結論:①AD=BE=5cm;②當0<t≤5時,![]() ;③直線NH的解析式為
;③直線NH的解析式為![]() ;④若△ABE與△QBP相似,則t=
;④若△ABE與△QBP相似,則t=![]() 秒。其中正確的結論個數為【 】
秒。其中正確的結論個數為【 】
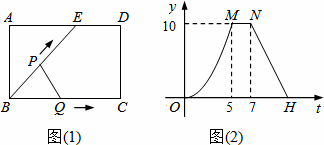
A. 4 B. 3 C. 2 D. 1
B。
【解析】根據圖(2)可得,當點P到達點E時點Q到達點C,
∵點P、Q的運動的速度都是1cm/秒,
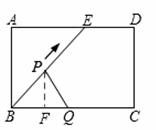
∴BC=BE=5cm。∴AD=BE=5,故結論①正確。
如圖1,過點P作PF⊥BC于點F,
根據面積不變時△BPQ的面積為10,可得AB=4,
∵AD∥BC,∴∠AEB=∠PBF。
∴![]() 。
。
∴PF=PBsin∠PBF=![]() t。
t。
∴當0<t≤5時,y=![]() BQ•PF=
BQ•PF=![]() t•
t•![]() t=
t=![]() 。故結論②正確。
。故結論②正確。
根據5~7秒面積不變,可得ED=2,
當點P運動到點C時,面積變為0,此時點P走過的路程為BE+ED+DC=11,故點H的坐標為(11,0)。
設直線NH的解析式為y=kx+b,
將點H(11,0),點N(7,10)代入可得:![]() ,解得:
,解得: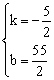 。
。
∴直線NH的解析式為:![]() 。故結論③錯誤。
。故結論③錯誤。
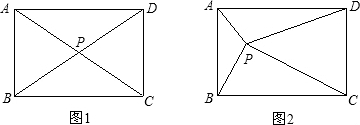
如圖2,當△ABE與△QBP相似時,點P在DC上,
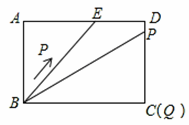
∵tan∠PBQ=tan∠ABE=![]() ,∴
,∴![]() ,即
,即![]() 。
。
解得:t=![]() 。故結論④正確。
。故結論④正確。
綜上所述,①②④正確,共3個。故選B。
考點:動點問題的函數圖象,雙動點問題,矩形的性質,銳角三角函數定義,待定系數法的應用,曲線上點的坐標與方程的關系,相似三角形的性質,分類思想的應用。


科目:初中數學 來源: 題型:
 系的圖象如圖2(曲線OM為拋物線的一部分),則下列結論:
系的圖象如圖2(曲線OM為拋物線的一部分),則下列結論:| 2 |
| 5 |
| 2 |
| 5 |
| 29 |
| 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2013年四川省南充市中考數學試卷(解析版) 題型:選擇題
 系的圖象如圖2(曲線OM為拋物線的一部分),則下列結論:
系的圖象如圖2(曲線OM為拋物線的一部分),則下列結論: t2;
t2; t+27;
t+27;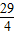 秒,
秒,查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(四川南充卷)數學(解析版) 題型:選擇題
(2013年四川南充3分)
如圖1,點E為矩形ABCD邊AD上一點,點P,點Q同時從點B出發,點P沿BE→ED→DC 運動到點C停止,點Q沿BC運動到點C停止,它們運動的速度都是1cm/s,設P,Q出發t秒時,△BPQ的面積為ycm,已知y與t的函數關系的圖形如圖2(曲線OM為拋物線的一部分),則下列結論:①AD=BE=5cm;②當0<t≤5時, ;③直線NH的解析式為
;③直線NH的解析式為 ;④若△ABE與△QBP相似,則t=
;④若△ABE與△QBP相似,則t=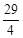 秒。其中正確的結論個數為【 】
秒。其中正確的結論個數為【 】

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com