
【題目】如圖1,在△ABC中,OB、OC是∠ABC、∠ACB的角平分線;
(1)填寫下面的表格.
∠A的度數 | 50° | 60° | 70° |
∠BOC的度數 |
(2)試猜想∠A與∠BOC之間存在一個怎樣的數量關系,并證明你的猜想;
(3)如圖2,△ABC的高BE、CD交于O點,試說明圖中∠A與∠BOD的關系.

【答案】(1)表格見解析(2)∠BOC=90°+![]() ∠A(3)證明見解析
∠A(3)證明見解析
【解析】(1)
∠A的度數 | 50° | 60° | 70° |
∠BOC的度數 | 115° | 120° | 125° |
(2)猜想:∠BOC=90°+![]() ∠A.
∠A.
理由:∵在△ABC中,OB、OC是∠ABC、∠ACB的角平分線;
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∵∠ABC+∠ACB=180°﹣∠A,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣![]() ∠A,
∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣![]() ∠A)=90°+
∠A)=90°+![]() ∠A.
∠A.
(3)證明:∵△ABC的高BE、CD交于O點,
∴∠BDC=∠BEA=90°,
∴∠ABE+∠BOD=90°,∠ABE+∠A=90°,
∴∠A=∠BOD.


科目:初中數學 來源: 題型:
【題目】若x0是方程ax2+2x+c=0(a≠0)的一個根,設M=1﹣ac,N=(ax0+1)2 , 則M與N的大小關系正確的為( )
A.M>N
B.M=N
C.M<N
D.不確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】AC是ABCD的一條對角線,過AC中點O的直線分別交AD,BC于點E,F.
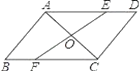
(1)求證:AE=CF;
(2)連接AF,CE.
①當EF和AC滿足條件 時,四邊形AFCE是菱形;
②若AB=1,BC=2,∠B=60°,則四邊形AFCE為矩形時,EF的長是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一只不透明的袋子中裝有3個球,球上分別標有數字0,1,2,這些球除了數字外其余都相同,甲、以兩人玩摸球游戲,規則如下:先由甲隨機摸出一個球(不放回),再由乙隨機摸出一個球,兩人摸出的球所標的數字之和為偶數時則甲勝,和為奇數時則乙勝.
(1)用畫樹狀圖或列表的方法列出所有可能的結果;
(2)這樣的游戲規則是否公平?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC的內切圓⊙O與AB、BC、CA分別相切于點D、E、F,且∠ACB=90°,AB=5,BC=3,點P在射線AC上運動,過點P作PH⊥AB,垂足為H.
(1)直接寫出線段AD及⊙O半徑的長;
(2)設PH=x,PC=y,求y關于x的函數關系式;
(3)當PH與⊙O相切時,求相應的y值.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,二次函數y=x2+(2k﹣1)x+k+1的圖象與x軸相交于O、A兩點.
(1)求這個二次函數的解析式;
(2)在這條拋物線的對稱軸右邊的圖象上有一點B,使銳角△AOB的面積等于3.求點B的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com