
 如圖,將在Rt△ABC繞其銳角頂點(diǎn)A旋轉(zhuǎn)90°得到在Rt△ADE,連接BE,延長DE、BC相交于點(diǎn)F,則有∠BFE=90°,且四邊形ACFD是一個正方形.
如圖,將在Rt△ABC繞其銳角頂點(diǎn)A旋轉(zhuǎn)90°得到在Rt△ADE,連接BE,延長DE、BC相交于點(diǎn)F,則有∠BFE=90°,且四邊形ACFD是一個正方形.| 1 |
| 2 |
| 1 |
| 2 |



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
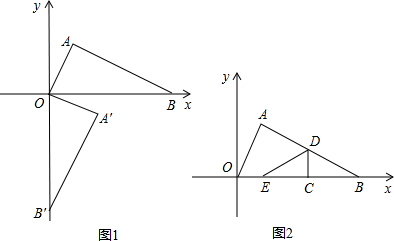 數(shù)關(guān)系式(包括自變量x的取值范圍).
數(shù)關(guān)系式(包括自變量x的取值范圍).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
| 2 |

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
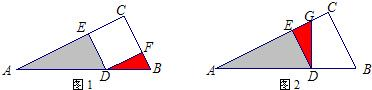
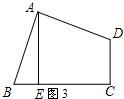
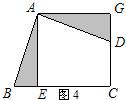
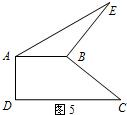
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
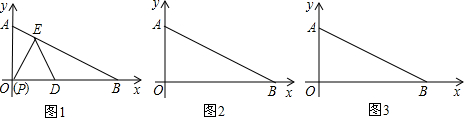
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com