Question

如果圓內接正六邊形的邊長為10cm，則它的邊心距為    cm，正六邊形的一邊在圓上截得的弓形面積是    cm²．

Answer 1

【答案】分析：（1）根據題意畫出圖形，利用等邊三角形的性質及銳角三角函數的定義直接計算即可；
（2）直接利用正六邊的一邊在圓上截得的弓形的面積減去三角形的面積即可解答．
解答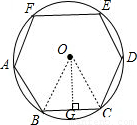：解：如圖所示，連接OB、OC過O作OG⊥BC于G，
∵此多邊形是正六邊形，
∴△OBC是等邊三角形，
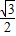
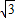
∴邊心距OG=OB•sin∠OBG=10×=5（cm²）；
∵正六邊的一邊在圓上截得的弓形的面積等于圓的面積減去三角形的面積，
∴S_弓形OBC=π×10²-×10×10×，
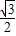
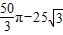
=（cm²）．
故答案分別為：5，．
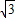
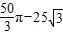
點評：本題考查的是正多邊形與圓、銳角三角函數的定義及特殊角的三角函數值，熟知正六邊形的性質是解答此題的關鍵．