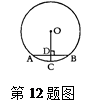
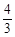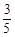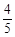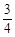如圖,AB是⊙O的直徑,弦CD⊥AB,垂足為E,連接AC、BC,若∠BAC=30º,CD=6cm.
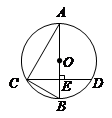
小題1:求∠BCD的度數(shù);
小題2:求⊙O的直徑.
小題1:∵直徑AB⊥CD,
∴⌒BC=⌒BD
∴∠DCB=∠CAB=30°
小題2:∵直徑AB⊥CD,CD=6,
∴CE=3……………………………………………… 4分
在Rt△ACE中,∠A=30°,
∴AC=6 ………………………………………………………………6分
∵AB是直徑,∴∠ACB=90°
在Rt△ACB中,AB===4(cm)
(1)由垂徑定理知,

=
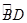
,∴∠DCB=∠CAB=30°;
(2)由垂徑定理知,點E是CD的中點,有CE=

CD=3,AB是直徑,∴∠ACB=90°,再求出AC的長,利用∠A的余弦即可求解.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:初中數(shù)學(xué)
來源:不詳
題型:解答題
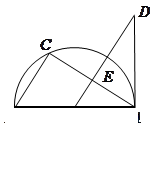
如圖,AB為半圓O的直徑,點C在半圓O上,過點O作BC的平行線交AC于點E,交過點A的直線于點D,且∠D=∠BAC.
小題1:求證:AD是半圓O的切線;
小題2:若BC=2,CE=
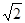
,求AD的長.
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,已知
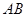
為⊙O的弦(非直徑),
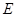
為
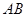
的中點,
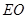
的延長線交圓于點
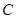
,
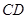
∥
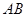
,且交
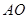
的延長線于點
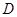
.
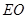
:
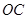
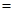
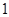
:
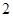
,
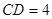
。求⊙O的半徑.
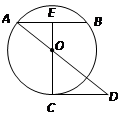
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:填空題
如圖,兩個同心圓的圓心是O,AD是大圓的直徑,大圓的弦AB,BE分別與小圓相切于點C,F(xiàn),連結(jié)BD,則∠ABE+2∠D=
。
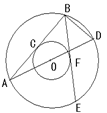
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:單選題
如圖,是一個工件的三視圖,則此工件的全面積是
| A.85πcm2 | B.90πcm2 | C.155πcm2 | D.165πcm2 |
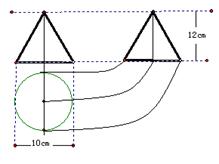
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:填空題
如圖是小明制作的一個圓錐形紙帽的示意圖.圍成這個紙帽的紙的側(cè)面積為
cm
2.
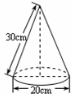
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:單選題
如圖,正方形ABCD中,E是BC邊上一點,以E為圓心、EC為半徑的半圓與以A為圓心,AB為半徑的圓弧外切,則sin∠EAB的值為
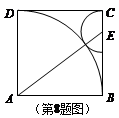
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:填空題
已知兩圓相交,它們的半徑分別為3和6,則這兩圓的圓心距d的取值滿足
查看答案和解析>>
科目:初中數(shù)學(xué)
來源:不詳
題型:填空題
如圖,AB為⊙O的弦,⊙O的半徑為5,OC⊥AB于點D,交⊙O于點C,且CDl,則弦AB的長是
。
查看答案和解析>>


 閱讀快車系列答案
閱讀快車系列答案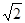 ,求AD的長.
,求AD的長.