
如圖,在一張透明的紙上畫了一個∠BAC,且∠BAC=α.


(1)如圖2,把紙片∠BAC沿DE折起(DE為折痕),使頂點A在∠BAC的內部,點A的對稱點為點O,求證:∠CDO+∠OEB=2α.
(2)如圖3,把紙片∠BAC沿DE折起(DE為折痕),使頂點A在∠BAC的外部,點A的對稱點為點O寫出∠CDO、∠OEB與α的等式關系(只寫出答案,無需證明).
(3)如圖4,在圖2的基礎上再以FG為折痕疊紙片,使頂點D、E在∠BAC的內部,且點D、E的對稱點分別為點P、Q,求∠CFP+∠PMO+∠ONQ+∠QGB的大小.
(4)如圖5,是一個側“M”形HUKL.已知:∠HIJ+∠JKL=2∠IJK.分別延長HI、LK交于點R,問∠HRL與∠IJK是否相等?如果相等,則請證明;如果不相等,則說明理由(舉一反例).
【考點】幾何變換綜合題.
【分析】(1)由平角和對折的性質簡單計算∠CDO=180°﹣2∠ADE即可;
(2)由平角和對折的性質簡單計算∠OEB=∠AED﹣180°即可;
(3)由對折和平角的意義進行簡單的計算,
(3)利用幾何圖形,對折,平角的意義簡單的計算.
【解答】解:(1)∵如圖2,
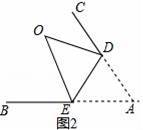

∵把三角形紙片ABC的∠A沿DE折起,點A的對稱點為點O,
∴∠CDO+∠OEB
=(180°﹣2∠ADE)+(180°﹣2∠AED)
=2(180°﹣∠ADE﹣∠AED)=2α;
(2)∠CDO﹣∠OEB=2α,
理由如下:如圖3,


∠CD0﹣∠OEB
=(180°﹣2∠ADE)﹣(2∠AED﹣180°)
=2(180°﹣∠ADE﹣∠AED)
=2α;
(3)∠CFP+PMO+∠ONQ+∠QGB=4α,
理由如下:如圖4,
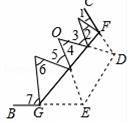

∠CFP+∠PMO+∠ONQ+∠QGB
=(∠CFP+∠PMO)+(∠ONQ+QGB)
=2∠FDM+2∠NEG
=2(∠FDM+NEG)
=4∠BAC
=4α;
(4)∠HRL=∠IJK,
理由如下:如圖5,


∵∠HIJ+∠JKL
=(∠IRJ+∠IJR)+(∠KRJ+∠KJR)
=(∠IJR+∠KJR)+(∠IRJ+∠KRJ)
=∠IJK+∠IRK
=2∠IJK,
∴∠HRL=∠IJK.
【點評】本題是幾何變換題,主要考查了對折的性質,本題的關鍵是從復雜圖形分離出有用的部分,本題易出錯的地方是,寫錯角.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
從甲,乙,丙三個廠家生產的同一種產品中,各抽出8件產品對其使用壽命(單位:年)進行跟蹤調查,結果如下:
甲:3,4,5,6,8,8,8,10;
乙:4,6,6,6,8,9,12,14.
丙:3,3,3,7,9,10,10,11.
三個廠家在廣告中都稱產品的使用壽命是8年,請根據調查結果判斷廠家在廣告中分別運用平均數,眾數,中位數中的哪一種集中趨勢的特征數?假若你作為消費 者,單純從耐用的角度會選擇哪種產品?
者,單純從耐用的角度會選擇哪種產品?
查看答案和解析>>
科目:初中數學 來源: 題型:
某商場為了促銷,凡購買1000元商品的顧客獲抽獎券一張.抽獎活動設置了如下的電翻獎牌,一張抽獎券只能有一次機會在9個數字中選中一個翻牌,其對應的反面就是獎品(重新啟動會自動隨機交換位置).
(1)求一張抽獎券翻到一臺電風扇的概率;
(2)有兩張抽獎券翻獎牌,請你根據題意寫出一個事件,使這個事件發生的概率是
 .
.
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
翻獎牌正面
| 一臺電風扇 | 一臺收音機 | 謝謝參與 |
| 謝謝參與 | 一副球拍 | 一個U盤 |
| 兩張電影票 | 謝謝參與 | 一副球拍 |
翻獎牌反面.
查看答案和解析>>
科目:初中數學 來源: 題型:
甲乙兩種水稻實驗品種連續5年的平均單位面積產量如下(單位:噸/公頃):

經計算, =10,
=10, =10,試根據這組數據估計__________種水稻品種的產量比較穩定.
=10,試根據這組數據估計__________種水稻品種的產量比較穩定.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com