【題目】根據國家發改委實施“階梯電價”的有關文件要求，某縣結合地方實際，決定對居民生活用電實行“階梯電價”收費，具體收費標準見下表
一戶居民一個月用電量的范圍 | 電費價格（單位：元/千瓦時） |
不超過150千瓦時的部分 | a |
超過150千瓦時，但不超過230千瓦時的部分 | b |
超過230千瓦時的部分 | a+0.33 |
2019年10月份，該縣居民甲用電100千瓦時，交費64元；居民乙用電200千瓦時，交費134.5元．
（1）根據題意，求出上表中a和b的值；
（2）實行“階梯電價”收費以后，該縣居民當月用電多少千瓦時時，其當月的平均電價為0.67元？
【答案】（1）a=0.64，b=0.77；（2）該縣居民當月用電195千瓦時時，其當月的平均電價為0.67元
【解析】
（1）根據“該縣居民甲用電100千瓦時，交費64元；居民乙用電200千瓦時，交費134．5元”，即可得出關于a，b的二元一次方程組，解之即可得出結論；
（2）設該縣居民當月用電x千瓦時時，其當月的平均電價為0.67元，分x≤150，150＜x≤230及x＞230三種情況，根據總價＝單價×數量，即可得出關于x的一元一次方程，解之即可得出結論．
解：（1）依題意，得：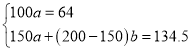
，
解得：
；
（2）設該縣居民當月用電x千瓦時時，其當月的平均電價為0．67元．
當x≤150時，0．64x＝0．67x，方程不成立；
當150＜x≤230時，150×0．64+0．77（x﹣150）＝0．67x，
解得：x＝195；
當x＞230時，150×0．64+（230﹣150）×0．77+（0．64+0．33）（x﹣230）＝0．67x，
解得：x＝
（不合題意，舍去）．
答：該縣居民當月用電195千瓦時時，其當月的平均電價為0．67元．
課堂全解字詞句段篇章系列答案
步步高口算題卡系列答案
點睛新教材全能解讀系列答案科目：初中數學 來源： 題型：
【題目】定義：若拋物線L2：y=mx2+nx（m≠0）與拋物線L1：y=ax2+bx（a≠0）的開口大小相同，方向相反，且拋物線L2經過L1的頂點，我們稱拋物線L2為L1的“友好拋物線”．
（1）若L1的表達式為y=x2﹣2x，求L1的“友好拋物線”的表達式；
（2）已知拋物線L2：y=mx2+nx為L1：y=ax2+bx的“友好拋物線”．求證：拋物線L1也是L2的“友好拋物線”；
（3）平面上有點P（1，0），Q（3，0），拋物線L2：y=mx2+nx為L1：y=ax2的“友好拋物線”，且拋物線L2的頂點在第一象限，縱坐標為2，當拋物線L2與線段PQ沒有公共點時，求a的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：矩形ABCD中，AB＝4，BC＝3，點M、N分別在邊AB、CD上，直線MN交矩形對角線 AC于點E，將△AME沿直線MN翻折，點A落在點P處，且點P在射線CB上.
(1)如圖1，當EP⊥BC時，求CN的長；
(2) 如圖2，當EP⊥AC時，求AM的長；
(3) 請寫出線段CP的長的取值范圍，及當CP的長最大時MN的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
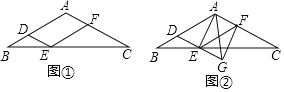
【題目】如圖①，在△ABC中，AB=AC，過AB上一點D作DE∥AC交BC于點E，以E為頂點，ED為一邊，作∠DEF=∠A，另一邊EF交AC于點F．
（1）求證：四邊形ADEF為平行四邊形；
（2）當點D為AB中點時，判斷ADEF的形狀；
（3）延長圖①中的DE到點G，使EG=DE，連接AE，AG，FG，得到圖②，若AD=AG，判斷四邊形AEGF的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校進行校園美化工程招標時，有甲、乙兩個工程隊投標，經測算：甲隊單獨完成這項工程需要60天，如果由甲隊先做20天，剩下的工程由甲、乙合作24天完成．
（1）乙隊單獨完成這項工程需要多少天？
（2）甲隊施工一天，需要支付工程款3.5萬元，乙隊施工一天需要支付工程款2萬元：如果規定在70天內完成這項工作，是由甲、乙兩隊單獨完成省錢？還是由甲乙合作完成該工程省錢？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知A
，B（-1,2）是一次函數
與反比例函數
（
）圖象的兩個交點，AC⊥x軸于C，BD⊥y軸于D．
(1)根據圖象直接回答：在第二象限內，當x取何值時，一次函數大于反比例函數的值?
(2)求一次函數解析式及m的值；
(3)P是線段AB上的一點，連接PC，PD，若△PCA和△PDB面積相等，求點P坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若點A（2，3）在反比例函數y＝
的圖象上，則下列說法正確的是（ ）
A.該函數圖象分布在第二、四象限
B.k的值為6
C.該函數圖象經過點（1，﹣6）
D.若點A（x1，y1），B（x2，y2）都在該函數圖象上，且x1＜x2，則y1＞y2
查看答案和解析>>
科目：初中數學 來源： 題型：
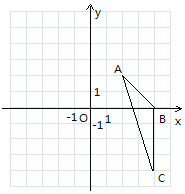
【題目】如圖，在平面直角坐標系中，已知△ABC三個頂點的坐標分別為A（2，2），B（4,0），C（4，-4）.
（1）請在圖中畫出△ABC向左平移6個單位長度后得到的△A1B1C1；
（2）以點O為位似中心，將△ABC縮小為原來的
，得到△A2B2C2，請在圖中y軸右側畫出△A2B2C2,；
（3）填空：△AA1A2的面積為________________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】
在平面直角坐標系的位置如圖所示．
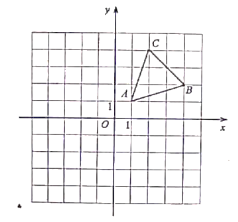
請作出關于
軸的對稱圖形
,再作出關于
軸的對稱圖形
;
若點
為邊
上一點，則點
在上的對應點的坐標為_ ;
點
為軸上一點，且點到點
的距高之和最短，請畫出圖形并寫出點的坐標為_ ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com