分析:作出圖形,連接OP,根據軸對稱的性質可得OP1=OP=OP2,∠BOP=∠BOP1,∠AOP=∠AOP2,然后求出∠P1OP2=2∠AOB=60°,再根據有一個角是60°的等腰三角形是等邊三角形判定.
解答: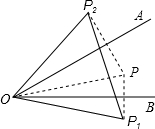
解:如圖,連接OP,
∵P
1與P關于OB對稱,P
2與P關于OA對稱,
∴OP
1=OP,OP=OP
2,∠BOP=∠BOP
1,∠AOP=∠AOP
2,
∴OP
1=OP
2,
∠P
1OP
2=∠BOP+∠BOP
1+∠AOP+∠AOP
2=2∠BOP+2∠AOP=2∠AOB,
∵∠AOB=30°,
∴∠P
1OP
2=60°,
∴△P
1OP
2是等邊三角形.
故答案為:等邊.
點評:本題考查了軸對稱的性質,等邊三角形的判定,熟練掌握軸對稱的性質求出△P1OP2的兩邊相等且有一個角是60°是解題的關鍵,作出圖形更形象直觀.

 解:如圖,連接OP,
解:如圖,連接OP,
