
已知如下圖,D、E分別是△ABC的AB、AC邊的中點,BE、CD相交于點F.
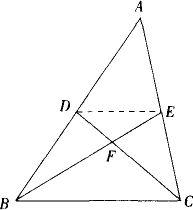
(1)求證:S四邊形ADFE=S△BCF;
(2)若SABC=24,求S四邊形ADFE.
|
(1)證明:∵D、E分別是AB、AC中點, ∴S△BCD=S△AEB= ∴S△BCD-S△BFD=S△AEB-S△BFD, 即 S四邊形ADFE=S△BCF. (2)解:連結DE,易知四邊形DBCE是梯形. 設S△BCF=x, ∵S△BED= S△BCD= ∴S△BFD=S△BCD-S△BCF=12-x, ∴SDFE=S△BED-S△BFD=6-(12-x), 根據性質2,有 (SBFD)2=S△BCF·S△DFE, ∴(12-x)2=x[6-(12-x)], 解得x=8. ∴S四邊形ADFE=S△BCF=8. 分析:(1)抓住D、E分別為AB、AC中點,用面積關系探求.(2)在(1)的基礎上,轉求S△BCF通過設未知數,用性質2建立方程進行探求. |


科目:初中數學 來源: 題型:閱讀理解
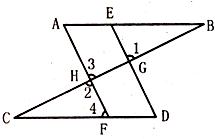 23、閱讀下面解答過程,并填空或填理由.
23、閱讀下面解答過程,并填空或填理由.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
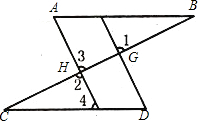
查看答案和解析>>
科目:初中數學 來源:四川省期末題 題型:解答題
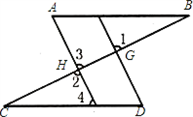
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com