
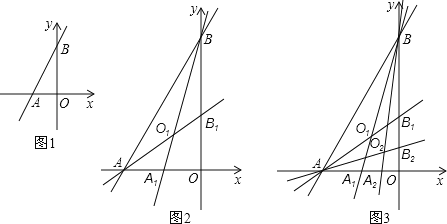
【題目】如圖1,一次函數y=2x+4與x軸,y軸分別相交于A,B兩點,一次函數圖象與坐標軸圍成的△ABO,我們稱它為此一次函數的坐標三角形.把坐標三角形面積分成相等的二部分的直線叫做坐標三角形的等積線.
(1)求此一次函數的坐標三角形周長以及過點A的等積線的函數表達式;
(2)如圖2,我們把第一個坐標三角形△ABO記為第一代坐標三角形.第一代坐標三角形的等積線BA1,AB1記為第一對等積線,它們交于點O1,四邊形A1OB1O1稱為第一個坐標四邊形.求點O1的坐標和坐標四邊形A1OB1O1面積;
(3)如圖3.第一對等積線與坐標軸構成了第二代坐標三角形△BA1O.△AOB1分別過點A,B作一條平分△BA1O,△AOB1面積的第二對等積線BA2,AB2,相交于點O2,如此進行下去.…,請直接寫出On的坐標和第n個坐標四邊形面積(用n表示).
【答案】(1)周長為6+2![]() ;等積線的函數表達式:y=x+2;(2)
;等積線的函數表達式:y=x+2;(2)![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)令y=0求出x的值,令x=0求出x的值,從而得到點A、B的坐標,再求出OA、OB的長,然后利用勾股定理列式求出AB,再根據三角形的周長公式列式計算即可得解;根據等積線的定義求出A1、B1的坐標,然后利用待定系數法求一次函數解析式解答;
(2)聯立兩等積線解析式求解即可得到O1的坐標,再根據坐標四邊形A1OB1O1面積=S△AOB1-S△AA1O1,列式計算即可得解;
(3)根據等積線的定義求出OAn、OBn,從而得到An、Bn的坐標,再利用待定系數法寫出ABn、BAn的解析式,聯立求解即可得到點On的坐標,再根據坐標四邊形面積=S△AOBn-S△AAnOn,列式計算即可得解.
試題解析:(1)令y=0,則2x+4=0,
解得,x=﹣2,
令x=0,則y=4,
∴點A(﹣2,0),B(0,4),
∴OA=2,OB=4,
由勾股定理得,AB=![]()
所以,周長為6+2![]()
∵AB1、BA1是等積線,
∴A1(﹣1,0),B1(0,2),
∴等積線的函數表達式:y=x+2;
(2)聯立![]()
解得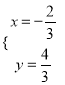 ,
,
∴O1(![]() ,
, ![]() ),
),
坐標四邊形A1OB1O1面積=S△AOB1﹣S△AA1O1,
=![]() ×2×2﹣
×2×2﹣![]() ×(2﹣1)×
×(2﹣1)×![]() ,
,
=2﹣![]() ,
,
=![]() ;
;
(3)由題意得,OAn=![]() ,OBn=
,OBn=![]() ,
,
所以,等積線BAn的解析式為:y=2n+1x+4,
ABn的解析式為:y=![]() x+
x+![]() ,
,
聯立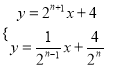 ,解得
,解得 ,
,
∴點On(﹣![]() ,
, ![]() ),
),
坐標四邊形面積=S△AOBn﹣S△AAnOn,
=![]() ×2×
×2×![]() ﹣
﹣![]() ×(2﹣
×(2﹣![]() )×
)×![]() ,
,
=![]() ﹣
﹣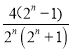 ,
,
=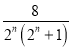 ,
,
=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在電線桿CD上的C處引拉線CE、CF固定電線桿,拉線CE和地面所成的角∠CED=60°,在離電線桿6米的B處安置高為1.5米的測角儀AB,在A處測得電線桿上C處的仰角為30°,求拉線CE的長(結果保留小數點后一位,參考數據: ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,已知![]() ,
,![]() ,可得
,可得![]() =______;
=______;
(2)如圖2,在(1)的條件下,如果![]() 平分
平分![]() ,則
,則![]() =________;
=________;
(3)如圖3,在(1)(2)的條件下,如果![]() ,則
,則![]() =_________;
=_________;
(4)嘗試解決下面問題:如圖4,![]() ,
,![]() ,
,![]() 是
是![]() 的平分線,
的平分線,![]() ,求
,求![]() 的度數.
的度數.




查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年,新疆某次足球聯賽規定每隊勝一場得3分,平一場得1分,負一場得0分,某隊前14場保持不敗,共得32分,設該隊平了x場,根據題意列方程得:_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】感知:如圖1,在△ABC中,∠ABC=42°,∠ACB=72°,點D是AB上一點,E是AC上一點,BE、CD相交于點F.
(1)若∠ACD=35°,∠ABE=20°,求∠BFC的度數;
(2)若CD平分∠ACB,BE平分∠ABC,求∠BFC的度數;
探究:如圖2,在△ABC中,BE平分∠ABC,CD平分∠ACB,寫出∠BFC與∠A之間的數量關系,并說明理由;
應用:如圖3,在△ABC中,BD平分∠ABC ,CD平分外角∠ACE,請直接寫出∠BDC與∠A之間的數量關系.



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】北京奧運會體育場的“鳥巢”鋼結構工程施工建設中,首次使用了我國科研人員自主研制的強度為4.6×108帕的鋼材,那么它的原數是( )
A.4600000B.46000000C.460000000D.4600000000
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com