
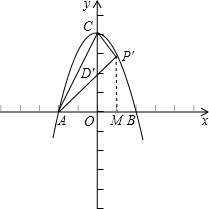
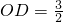 ,試比較S△APC與S△AOC的大小;
,試比較S△APC與S△AOC的大小;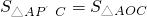 ?若存在,請求出點P′的坐標;若不存在,請說明理由.
?若存在,請求出點P′的坐標;若不存在,請說明理由.
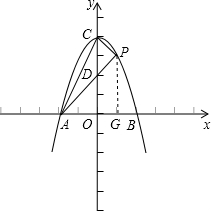 解:(1)由
解:(1)由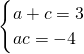
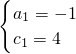 或
或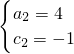 ,
,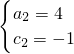 (不合題意,舍去),
(不合題意,舍去), ,
,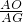 =
=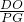 ,
,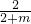 =
=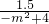 ,
, ,m2=-2(舍去),
,m2=-2(舍去), .
. CD•GO=
CD•GO= ×
× ×
× =
= ,
, AO•DO=
AO•DO= ×2×
×2× =
=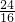 ,
,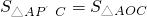 ,
,
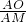 =
=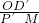 ,即
,即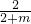 =
=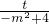 ,
, CD′•OM=
CD′•OM= (4-t)•m,
(4-t)•m, OA•OD′=
OA•OD′= ×2•t=t,
×2•t=t,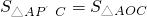 ,
,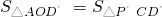 ,
, (4-t)m,即mt+2t=4m ②
(4-t)m,即mt+2t=4m ② -1,m2=-
-1,m2=- -1(不合題意舍去),
-1(不合題意舍去),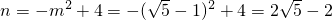 .
. -1,2
-1,2 -2),
-2),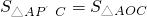 .
. ,再利用已知求出S△PDC,S△AOD的面積,進而得出S△APC與S△AOC的大小關系;
,再利用已知求出S△PDC,S△AOD的面積,進而得出S△APC與S△AOC的大小關系;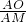 =
=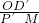 ,以及利用三角形面積關系得出
,以及利用三角形面積關系得出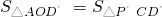 ,進而求出m的值,即可求出點P′的坐標.
,進而求出m的值,即可求出點P′的坐標.

 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:初中數學 來源: 題型:
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com