

 t2,
t2, -
- (2-t)2=-
(2-t)2=- t2+2
t2+2 t-
t- ,
, ;
; ),B(5,
),B(5, ),拋物線對稱軸為x=3,
),拋物線對稱軸為x=3,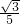 ,∴y=-
,∴y=-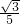 x(x-6)=-
x(x-6)=-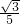 x2+
x2+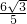 x,
x, x,
x, x+k,
x+k, (t-5),
(t-5), x+
x+ (t-5),
(t-5),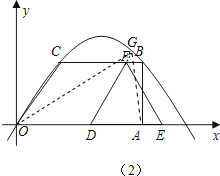
 ×5×h=
×5×h= ×(4+5)×
×(4+5)× ,
,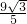 ,
,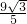 代入y=-
代入y=-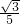 x(x-6)中,得x=3,
x(x-6)中,得x=3, ),
), x+
x+ (t-5)中,得t=3.8,
(t-5)中,得t=3.8,

科目:初中數學 來源: 題型:
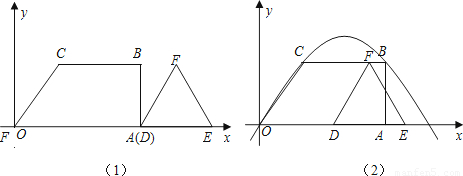
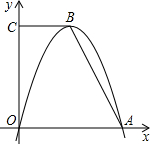 如圖,在梯形OABC中,CB∥OA,O為坐標原點,點C在y軸上,點A在x軸上,OC=4,tan∠OAB=2,以點B為頂點的拋物線經過O、A兩點.求梯形OABC的面積.
如圖,在梯形OABC中,CB∥OA,O為坐標原點,點C在y軸上,點A在x軸上,OC=4,tan∠OAB=2,以點B為頂點的拋物線經過O、A兩點.求梯形OABC的面積.查看答案和解析>>
科目:初中數學 來源: 題型:
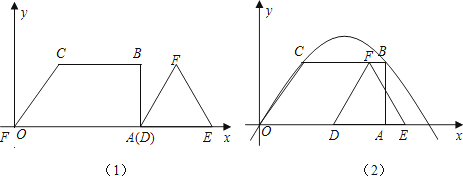
查看答案和解析>>
科目:初中數學 來源:2013年河北省邯鄲市中考數學模擬試卷(一)(解析版) 題型:解答題
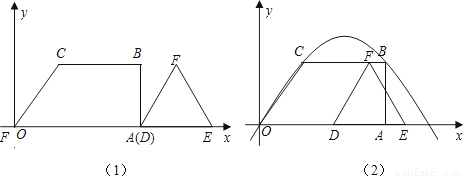
查看答案和解析>>
科目:初中數學 來源:2011年甘肅省天水市中考數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com