
【題目】如圖,在平面直角坐標系xOy中,矩形OEFG的頂點E的坐標為(4,0),頂點G的坐標為(0,2),將矩形OEFG繞點O逆時針旋轉,使點F落在y軸的點N處,得到矩形OMNP,OM與GF交于點A.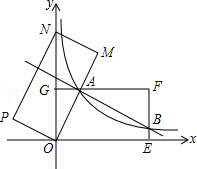
(1)求圖象經過點A的反比例函數的解析式;
(2)設(2)中的反比例函數圖象交EF于點B,直接寫出直線AB的解析式.
【答案】
(1)
解:∵∠OGA=∠M=90°∠GOA=∠MON
∴△OGA∽△OMN,
∴ ![]()
∴ ![]() ,
,
解得AG=1.
設反比例函數y= ![]() ,把A(1,2)代入得k=2,
,把A(1,2)代入得k=2,
∴過點A的反比例函數的解析式為:y= ![]() .
.
(2)
解:∵點B的橫坐標為4,x=4代y= ![]() 中y=
中y= ![]() ,故(4,
,故(4, ![]() )
)
設直線AB的解析式y=mx+n,把A(1,2)、B(4, ![]() )代入,得
)代入,得
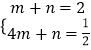 ,
,
解得 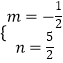 .
.
∴直線AB的解析式y=﹣ ![]() x+
x+ ![]() .
.
【解析】(1)先根據兩個角對應相等,即可證明△OGA和△OMN相似,要求反比例函數的解析式,則需求得點A的坐標,即要求得AG的長,根據旋轉的兩個圖形全等的性質以及相似三角形的對應邊的比相等可以求解;(2)要求直線AB的解析式,主要應求得點B的坐標.根據點B的橫坐標是4和(1)中求得的反比例函數的解析式即可求得.再根據待定系數法進行求解.
【考點精析】本題主要考查了反比例函數的性質的相關知識點,需要掌握性質:當k>0時雙曲線的兩支分別位于第一、第三象限,在每個象限內y值隨x值的增大而減小; 當k<0時雙曲線的兩支分別位于第二、第四象限,在每個象限內y值隨x值的增大而增大才能正確解答此題.


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中,A(-1,5)、B(-1,0)、C(-4,3)
(1) 求出△ABC的面積
(2) 在圖形中作出△ABC關于y軸的對稱圖形△A1B1C1,并寫出A1、B1、C1的坐標
(3) 是否存在一點P到AC、AB的距離相等,同時到點A、點B的距離也相等.若存在保留作圖痕跡標出點P的位置,并簡要說明理由;若不存在,請說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一個供滑板愛好者使用的U型池,該U型池可以看作是一個長方體去掉一個“半圓柱”而成,中間可供滑行部分的截面是半徑為4 m的半圓,其邊緣AB=CD=20 m,點E在CD上,CE=4 m,一滑行愛好者從A點滑到E點,則他滑行的最短距離是多少?(邊緣部分的厚度可以忽略不計,π取3)

查看答案和解析>>
科目:初中數學 來源: 題型:
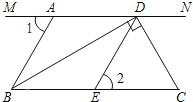
【題目】如圖,MN∥BC,BD⊥DC,∠1=∠2=60°.
(1)AB 與 DE 平行嗎?請說明理由;
(2)若 DC 是∠NDE 的平分線.
①試說明∠ABC=∠C;
②試說明 BD 是∠ABC 的平分線.
查看答案和解析>>
科目:初中數學 來源: 題型:
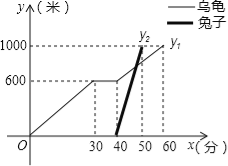
【題目】“龜兔首次賽跑”之后,輸了比賽的兔子沒有氣餒,總結反思后,和烏龜約定再賽一場.圖中的函數圖象刻畫了“龜兔再次賽跑”的故事(x表示烏龜從起點出發所行的時間,y1表示烏龜所行的路程,y2表示兔子所行的路程).有下列說法:
①“龜兔再次賽跑”的路程為1000米;
②兔子和烏龜同時從起點出發;
③烏龜在途中休息了10分鐘;
④兔子在途中750米處追上烏龜.
其中正確的說法是 .(把你認為正確說法的序號都填上)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+bx+c經過A(﹣1,0),C(0,4)兩點,與x軸交于另一點B,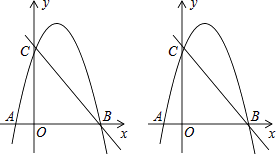
(1)求拋物線的解析式;
(2)求P在第一象限的拋物線上,P點的橫坐標為t,過點P向x軸做垂線交直線BC于點Q,設線段PQ的長為m,求m與t之間的函數關系式并求出m的最大值;
(3)在(2)的條件下,拋物線上一點D的縱坐標為m的最大值,連接BD,在拋物線是否存在點E(不與點A,B,C重合)使得∠DBE=45°?若不存在.請說明理由;若存在請求E點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一間階梯教室,第1排的座位數為a,從第2排開始,每一排都比前一排增加b個座位,
(1)請你在下表的空格里填寫一個適當的式子:
第1排座位數 | 第2排座位數 | 第3排座位數 | 第4排座位數 | …… |
a | a+b | a+2b` | …… |
(2)已知第4排有18個座位,第15排的座位數是第5排座位數的2倍,求第21排有多少個座位?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廣電局與長江證券公司聯合推出廣電寬帶網業務,用戶通過寬帶網可以享受新聞點播、影視欣賞、股市大戶室等項服務,用戶繳納上網費的方式有:方式一:每月80元包月;方式二:每月上網費y(元)與上網時間x(小時)的函數關系用如圖所示的折線表示;方式三:以0小時為起點,每小時收費1.6元,月收費不超過120元.若設一用戶每月上網x小時,月上網費為y元.

(1)根據圖象,寫出方式二中y(元)與x(小時)的函數關系式;
(2)試寫出方式三中y(元)與x(小時)的函數關系式;
(3)若此用戶每月上網60小時,選用哪種方式上網其費用最少?最少費用是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com