
 =
=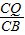 ,進而求出t的值即可;
,進而求出t的值即可; PC×CQ得出關于t的二次函數的解析式,進而求出最值即可;
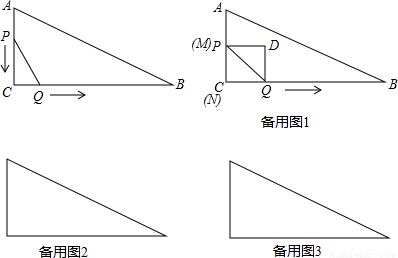
PC×CQ得出關于t的二次函數的解析式,進而求出最值即可;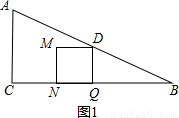 解:(1)由題意得出:CQ=t,PC=6-t,
解:(1)由題意得出:CQ=t,PC=6-t,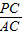 =
=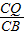 ,
,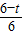 =
=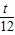 ,
, PC×CQ=-
PC×CQ=- t2+3t=-
t2+3t=- (t-3)2+
(t-3)2+ ;
; ;
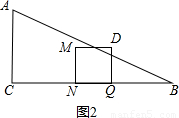
;
 =
=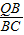 ,
,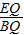 =
= ,
, t,
t, t-3,
t-3, DE×DF=-
DE×DF=- t2+3t;
t2+3t;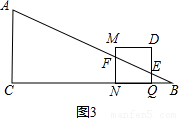
 (12-t),
(12-t), (15-t),
(15-t), (QE+FN)×3=-
(QE+FN)×3=- t+
t+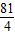 .
.

科目:初中數學 來源: 題型:
 如圖所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,點D在BC上運動(不能到達點B,C),過點D作∠ADE=45°,DE交AC于點E.
如圖所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,點D在BC上運動(不能到達點B,C),過點D作∠ADE=45°,DE交AC于點E.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com