已知關于x的方程x2-2(m+1)x+m2-2m-3=0的兩個不相等實根中有一個是0.
(1)請求出m的值;
(2)是否存在實數k,使關于x的方程x2-(k-m)x-k-m2+5m-2=0的兩個實根x1,x2之差的絕對值為1?若存在,求出k的值;若不存在,請說明理由.
【答案】
分析:(1)先根據△的意義得到m>-1,再把x=0代入方程x
2-2(m+1)x+m
2-2m-3=0得m
2-2m-3=0,解得m
1=3,m
2=-1,即可得到滿足條件的m的值;
(2)把m=3代入方程x
2-(k-m)x-k-m
2+5m-2=0得x
2-(k-3)x-k+4=0,根據根與系數的關系得到x
1+x
2=k-3,x
1x
2=-k+4,然后由|x
1-x
2︳=1變形得(x
1-x
2)
2=1,即(x
1+x
2)
2-4x
1x
2-1=0
再把x
1+x
2=k-3,x
1x
2=-k+4代入得到關于k的方程,然后解方程,若k有實數解并且使原方程也有解,就可判斷存在.
解答:解:(1)∵方程x
2-2(m+1)x+m
2-2m-3=0的兩個不相等實根,
∴△=4(m+1)
2-4(m
2-2m-3)>0,
∴m>-1,
把x=0代入方程x
2-2(m+1)x+m
2-2m-3=0得m
2-2m-3=0,
∵(m-3)(m+1)=0,
∴m
1=3,m
2=-1,
而m>-1,
∴m的值為3;
(2)存在.
把m=3代入方程x
2-(k-m)x-k-m
2+5m-2=0得
x
2-(k-3)x-k+4=0,
∴x
1+x
2=k-3,x
1x
2=-k+4,
∵|x
1-x
2︳=1,
∴(x
1-x
2)
2=1,即(x
1+x
2)
2-4x
1x
2-1=0
(k-3)
2-4(-k+4)-1=0,
整理得k
2-2k-8=0,
k
1=4,k
2=-2,
當k=4和-2時方程x
2-(k-3)x-k+4=0都有兩個實數,
∴存在實數k,使關于x的方程x
2-(k-m)x-k-m
2+5m-2=0的兩個實根x
1,x
2之差的絕對值為1.
點評:本題考查了一元二次方程ax
2+bx+c=0(a≠0)的根與系數的關系:若方程兩根為x
1,x
2,則x
1+x
2=-
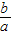
,x
1•x
2=
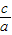
.也考查了一元二次方程根的判別式.

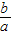 ,x1•x2=
,x1•x2=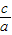 .也考查了一元二次方程根的判別式.
.也考查了一元二次方程根的判別式. 

 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案