
【題目】已知直線l1:y=﹣![]() 與直線l2:y=kx﹣
與直線l2:y=kx﹣![]() 交于x軸上的同一個點A,直線l1與y軸交于點B,直線l2與y軸的交點為C.
交于x軸上的同一個點A,直線l1與y軸交于點B,直線l2與y軸的交點為C.
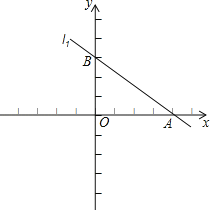
(1)求k的值,并作出直線l2圖象;
(2)若點P是線段AB上的點且△ACP的面積為15,求點P的坐標;
(3)若點M、N分別是x軸上、線段AC上的動點(點M不與點O重合),是否存在點M、N,使得△ANM≌△AOC?若存在,請求出N點的坐標;若不存在,請說明理由.
【答案】(1)k=![]() ,見解析;(2)點P的坐標(
,見解析;(2)點P的坐標(![]() ,
,![]() );(3)當N的縱坐標為(
);(3)當N的縱坐標為(![]() ,﹣
,﹣![]() )時,△ANM≌△AOC.
)時,△ANM≌△AOC.
【解析】
試題分析:(1)對于直線l1,令y=0求出x的值,確定出A坐標,代入直線l2求出k的值,作出直線l2圖象即可;
(2)設P(a,b),△ACP面積=△ABC面積﹣△BPC面積,根據已知三角形ACP面積求出a的值,進而求出b的值,確定出P坐標即可;
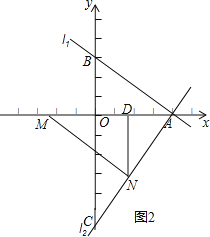
(3)如圖2,作ND⊥x軸于D,利用勾股定理求出AC的長,由△ANM≌△AOC,得到對應邊相等,表示出AM,AN,MN,確定出△AMN為直角三角形,利用面積法求出ND的長,確定出N縱坐標,進而求出橫坐標,確定出N坐標即可.
解:(1)∵直線l1:y=﹣![]() x+3與x軸交于點A,
x+3與x軸交于點A,
∴令y=0時,x=4,即A(4,0),
將A(4,0)代入直線l2:y=kx﹣![]() ,得k=
,得k=![]() ,
,
直線l2圖象如圖1所示;
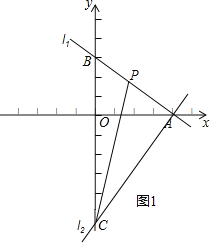
(2)設P(a,b),
根據題意得:S△ACP=S△ABC﹣S△PBC=![]() ×(3+
×(3+![]() )×4﹣
)×4﹣![]() ×(3+
×(3+![]() )a=15,
)a=15,
解得:a=![]() ,
,
將P(![]() ,b)代入直線l1得:b=
,b)代入直線l1得:b=![]() ×(﹣
×(﹣![]() )+3=﹣
)+3=﹣![]() +3=
+3=![]() ,
,
∴點P的坐標(![]() ,
,![]() );
);
(3)如圖2,作ND⊥x軸于D,
∵AC=![]() =
=![]() ,△ANM≌△AOC,
,△ANM≌△AOC,
∴AM=AC=![]() ,AN=AO=4,MN=OC=
,AN=AO=4,MN=OC=![]() ,∠ANM=∠AOC=90°,
,∠ANM=∠AOC=90°,
∵S△AMN=![]() AMND=
AMND=![]() ANMN,
ANMN,
∴ND=![]() =
=![]() =
=![]() ,
,
將N的縱坐標y=﹣![]() 代入直線l2得:x=
代入直線l2得:x=![]() ,
,
∴當N的縱坐標為(![]() ,﹣
,﹣![]() )時,△ANM≌△AOC.
)時,△ANM≌△AOC.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,點O是直線EF上一點,射線OA,OB,OC在直線EF的上方,射線OD的直線EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
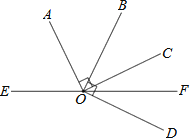
(1)若∠DOF=25°,求∠AOB的度數.
(2)若OA平分∠BOE,則∠DOF的度數是 .(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
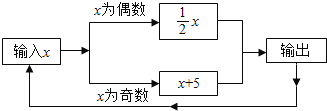
【題目】有一數值轉換機,原理如圖所示,若開始輸入x的值是7,可發現第1次輸出的結果是12,第2次輸出的結果是6,第3次輸出的結果是 ,依次繼續下去…,第2015次輸出的結果是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:數軸上A、B兩點表示的有理數分別為a、b,且(a﹣1)2+|b+2|=0,
(1)求(a+b)2015的值.
(2)數軸上的點C與A、B兩點的距離的和為7,求點C在數軸上表示的數c的值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋里裝有若干除顏色外其他完全相同的小球,其中有6個黃球,將口袋中的球搖勻,從中任意摸出一個球記下顏色后再放回,通過大量重復上述實驗后發現,摸到黃球的頻率穩定在30%,由此估計口袋中共有小球 個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,AC=BC,D為BC中點,CE⊥AD于E,BF∥AC交CE的延長線于F.

(1)求證:△ACD≌△CBF;
(2)求證:AB垂直平分DF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC中,a、b、c分別是∠A、∠B、∠C的對邊,下列條件不能判斷△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com