【題目】某市舉辦中學生“夢想杯”足球聯賽，聯賽記分辦法是：勝1場得3分，平1場得1分，負1場得0分.復興中學足球隊參加了18場比賽，積24分.
（1）在這次足球聯賽中，如果復興中學足球隊踢平場數與所負場數相同，那么它勝了幾場？
（2）在這次足球聯賽中，如果復興中學足球隊踢平場數多于所負場數，那么它的勝、平、負情況共有多少種？
科目：初中數學 來源： 題型：
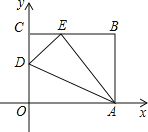
【題目】如圖，OABC是一張放在平面直角坐標系中的矩形紙片，O為原點，點A在x軸的正半軸上，點C在y軸的正半軸上，OA=10，OC=8，在OC邊上取一點D，將紙片沿AD翻折，使點O落在BC邊上的點E處，則D點的坐標是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
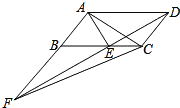
【題目】如圖，平行四邊形ABCD中，AE平分∠BAD，交BC于點E，且AB＝AE，延長AB與DE的延長線交于點F．下列結論中：①△ABC≌△AED；②△ABE是等邊三角形；③AD＝AF；④S△ABE＝S△CDE；⑤S△ABE＝S△CEF．其中正確的是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在數軸上點 A 表示的有理數為﹣4，點 B 表示的有理數為 6，點 P 從 點 A 出發以每秒 2 個單位長度的速度在數軸上沿由 A 到 B 方向運動，當點 P 到 達點 B 后立即返回，仍然以每秒 2 個單位長度的速度運動至點 A 停止運動．設 運動時間為 t（單位：秒）．
（1）求 t=2 時點 P 表示的有理數；
（2）求點 P 是 AB 的中點時 t 的值；
（3）在點 P 由點 A 到點 B 的運動過程中，求點 P 與點 A 的距離（用含 t 的代數式表示）；
（4）在點 P 由點 B 到點 A 的返回過程中，點 P 表示的有理數是多少（用含 t 的 代數式表示）．
查看答案和解析>>
科目：初中數學 來源： 題型：
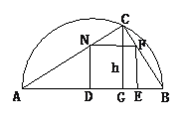
【題目】在直徑為AB的半圓內，劃出一塊三角形區域，如圖所示，使三角形的一邊為AB，頂點C在半圓圓周上，其它兩邊分別為6和8，現要建造一個內接于△ABC的矩形水池DEFN，其中D、E在AB上，如圖24-94的設計方案是使AC=8，BC=6．
（1）求△ABC的邊AB上的高h．
（2）設DN=x，且
，當x取何值時，水池DEFN的面積最大？
（3）實際施工時，發現在AB上距B點1．85的M處有一棵大樹，問：這棵大樹是否位于最大矩形水池的邊上？如果在，為了保護大樹，請設計出另外的方案，使內接于滿足條件的三角形中欲建的最大矩形水池能避開大樹．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在邊長為1個單位長度的小正方形網格中建立平面直角坐標系，已知
的頂點
的坐標為
，頂點
的坐標為
，頂點
的坐標為
.
（1）求的面積；
（2）若把向上平移3個單位長度，再向左平移6個單位長度得到
，請畫出；
（3）若點
在
軸上，且
的面積與的面積相等，請直接寫出點的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于正數
，規定
.
例如：
，
，
.
(1)求值：
=________ ；
__________
(2)猜想：
=___________ ，并證明你的結論；
(3)求：
的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P是∠AOB內任意一點，OP=5cm，點M和點N分別是射線OA和射線OB上的動點，△PMN周長的最小值是5cm，則∠AOB的度數是（ ）
A. 25° B. 30° C. 35° D. 40°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
