
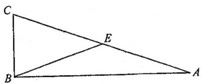
如圖,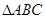 中,
中,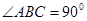 ,
,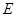 為
為 的中點.
的中點.
操作:過點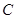 做
做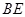 的垂線,過點
的垂線,過點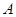 作
作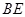 的平行線,兩直線相交于點
的平行線,兩直線相交于點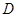 ,在
,在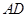 的延長線上截取
的延長線上截取 ,聯結
,聯結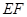 、
、 .
.

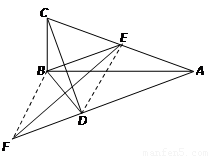
(1)試判斷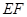 與
與 之間有怎樣的關系,并證明你所得的結論;
之間有怎樣的關系,并證明你所得的結論;
(2)如果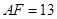 ,
, ,求
,求 的長.
的長.
解:如圖,(1)EF與BD互相垂直平分.
證明如下:連結DE、BF,∵BE //DF,
∴四邊形BEDF是平行四邊形.
∵CD⊥BE,∴CD⊥AD,
∵∠ABC=90º,E為AC的中點,
∴BE=DE=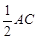 ,
,
∴四邊形BEDF是菱形.
∴EF與BD互相垂直平分.
(2)設DF=BE=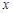 ,則AC=2
,則AC=2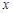 ,AD=AF–DF=13–
,AD=AF–DF=13–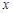 .
.
在Rt△ACD中,∵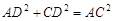 ,(1分)∴
,(1分)∴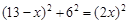 .
.


∴AC=10.
【解析】(1)證平行四邊形BEDF,根據直角三角形斜邊上的中線證BE=DF,推出菱形BEDF即可;
(2)設DF=BE=x,則AC=2x,AD=AF-DF=13-x,在Rt△ACD中根據勾股定理求出x,即可得到答案.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源:北京市大興區2008學年初三模擬檢測數學試卷 題型:044
矩形ABCD中,AD=2,2<AB<4,現將一個直徑MN為2的量角器如圖1擺放,使其0°線的端點N與C重合,M與B重合,O為MN的中點,量角器的半圓弧與矩形ABCD的對角線AC、BD分別交于P、Q,設P、Q在量角器上的讀數分別是x、y.
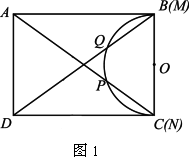
(1)求y與x之間的函數關系式.(不必寫出自變量的取值范圍).
(2)將量角器繞C點逆時針旋轉,使它的直徑落在AC上,如圖2所示,![]() 為
為![]() 的中點,此時量角器的半圓弧交DC于K,若K點的讀數為z,那么z與y的數量關系是什么,請說明理由.
的中點,此時量角器的半圓弧交DC于K,若K點的讀數為z,那么z與y的數量關系是什么,請說明理由.
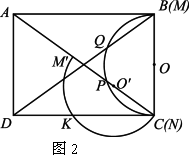
(3)如圖2所示,若![]() ∥KO,求出此時AB的長.
∥KO,求出此時AB的長.
查看答案和解析>>
科目:初中數學 來源:2012屆上海市奉賢區九年級調研測試數學試卷(帶解析) 題型:解答題
如圖, 中,
中, ,
,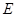 為
為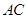 的中點.
的中點.
操作:過點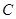 做
做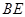 的垂線,過點
的垂線,過點 作
作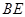 的平行線,兩直線相交于點
的平行線,兩直線相交于點 ,在
,在 的延長線上截取
的延長線上截取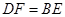 ,聯結
,聯結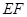 、
、 .
.

(1)試判斷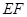 與
與 之間有怎樣的關系,并證明你所得的結論;
之間有怎樣的關系,并證明你所得的結論;
(2)如果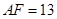 ,
,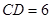 ,求
,求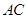 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點.
的中點.
操作:過點![]() 做
做![]() 的垂線,過點
的垂線,過點![]() 作
作![]() 的平行線,兩直線相交于點
的平行線,兩直線相交于點![]() ,在
,在![]() 的延長線上截取
的延長線上截取![]() ,聯結
,聯結![]() 、
、![]() .
.
(1)試判斷![]() 與
與![]() 之間有怎樣的關系,并證明你所得的結論;
之間有怎樣的關系,并證明你所得的結論;
(2)如果![]() ,
,![]() ,求
,求![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
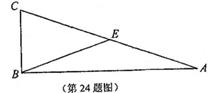
如圖,![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點.
的中點.
操作:過點![]() 做
做![]() 的垂線,過點
的垂線,過點![]() 作
作![]() 的平行線,兩直線相交于點
的平行線,兩直線相交于點![]() ,在
,在![]() 的延長線上截取
的延長線上截取![]() ,聯結
,聯結![]() 、
、![]() .
.
(1)試判斷![]() 與
與![]() 之間有怎樣的關系,并證明你所得的結論;
之間有怎樣的關系,并證明你所得的結論;
(2)如果![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com