證明:∵四邊形EFBC為矩形,
∴BF∥EC,BF=EC.
∴∠BFC=∠ECF.
∴∠AFB=∠DCE.
在△ABF與△DEC中
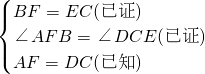
,
∴△ABF≌△DEC(SAS).
∴∠A=∠D.
∴AB∥DE.
分析:要證明AB∥ED,就要證明∠A=∠D,就要證明出△AFB≌△DCE,已知了AF=CD,根據矩形的性質,BF=CE,那么只要證明∠AFB=∠DCE,即∠CFB=∠FCE即可.那么可根據BF∥CE得出.
點評:判定兩個三角形全等,先根據已知條件或求證的結論確定三角形,然后再根據三角形全等的判定方法,看缺什么條件,再去證什么條件.
