
【題目】已知![]() ,
,![]() ,
,![]() 為正整數,
為正整數,![]() .設
.設![]() ,
,![]() ,
,![]() ,
,![]() 為坐標原點.若
為坐標原點.若![]() ,且
,且![]() .
.
(1)求圖象經過![]() ,
,![]() ,
,![]() 三點的二次函數的解析式;
三點的二次函數的解析式;
(2)點![]() 是拋物線上的一動點,直線
是拋物線上的一動點,直線![]() 交線段
交線段![]() 于點
于點![]() ,若
,若![]() ,
,![]() 的面積
的面積![]() ,
,![]() 滿足
滿足![]() ,求此時點
,求此時點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由射影定理得到![]() ,即
,即![]() ,然后代入到已知條件中得到
,然后代入到已知條件中得到![]() ,然后利用一元二次方程根與系數的關系求得
,然后利用一元二次方程根與系數的關系求得![]() ,
,![]() .利用待定系數法求二次函數解析式;
.利用待定系數法求二次函數解析式;
(2)由![]() 得
得![]() ,從而確定Q點坐標,然后利用待定系數法求得直線AQ的解析式,然后聯立方程組求點D坐標.
,從而確定Q點坐標,然后利用待定系數法求得直線AQ的解析式,然后聯立方程組求點D坐標.
解:(1)∵![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]()
![]() ,
,
![]()
![]()
∴![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() 是關于
是關于![]() 的一元二次方程
的一元二次方程![]() ①的兩個不相等的正整數根,
①的兩個不相等的正整數根,
∴![]() ,解得
,解得![]() .
.
又∵![]() 為正整數,故
為正整數,故![]() 或
或![]() .
.
當![]() 時,方程①為
時,方程①為![]() ,沒有整數解.
,沒有整數解.
當![]() 時,方程①為
時,方程①為![]() ,兩根為
,兩根為![]() ,
,![]() .
.
綜合知:![]() ,
,![]() ,
,![]() .
.
設圖象經過![]() ,
,![]() ,
,![]() 三點的二次函數的解析式為
三點的二次函數的解析式為![]() ,
,
將點![]() 的坐標代入得
的坐標代入得![]() ,解得
,解得![]() .
.
∴圖象經過![]() ,
,![]() ,
,![]() 三點的二次函數的解析式為
三點的二次函數的解析式為![]() .
.
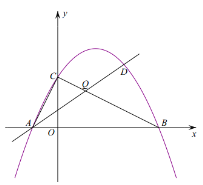
(2)如圖,直線![]() 交線段
交線段![]() 于點
于點![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
設直線AQ的解析式為y=kx+b
可得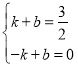 解得
解得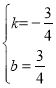
∴直線AQ的解析式為:![]() ,
,
聯立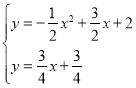 ,
,
消去![]() 整理可得,
整理可得,![]() ,
,
由韋達定理:![]() ,而
,而![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() 點坐標為:
點坐標為:![]() .
.


科目:初中數學 來源: 題型:
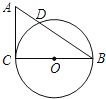
【題目】如圖,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC為直徑作⊙O交AB于點D.
(1)求線段AD的長度;
(2)點E是線段AC上的一點,試問:當點E在什么位置時,直線ED與⊙O相切?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2﹣2mx+m2﹣3(m是常數)
(1)證明:無論m取什么實數,該拋物線與x軸都有兩個交點.
(2)設拋物線的頂點為A,與x軸的兩個交點分別為B、D,點B在點D的右側,與y軸的交點為 C.
①若點P為△ABD的外心,求點P的坐標(用含m的式子表示);
②當|m|≤![]() ,m≠0時,△ABC的面積是否有最大值?如果有,請求出最大值;如果沒有,請說明理由.
,m≠0時,△ABC的面積是否有最大值?如果有,請求出最大值;如果沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店經銷A、B兩種商品,現有如下信息:
信息1:A、B兩種商品的進貨單價之和是3元;
信息2:A商品零售單價比進貨單價多1元,B商品零售單價比進貨單價的2倍少1元;
信息3:按零售單價購買A商品3件和B商品2件,共付12元.
請根據以上信息,解答下列問題:
(1)求A、B兩種商品的零售單價;
(2)該商店平均每天賣出A商品500件和B商品1500件.經調查發現,A種商品零售單價每降0.1元,A種商品每天可多銷售100件.商店決定把A商品的零售單價下降m(m>0)元,B商品的零售單價和銷量都不變,在不考慮其他因素的條件下,當m為多少時,商品每天銷售A、B兩種商品獲取的總利潤為2000元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】五張如圖所示的長為![]() ,寬為
,寬為![]() 的小長方形紙片,按如圖的方式不重疊地放在矩形
的小長方形紙片,按如圖的方式不重疊地放在矩形![]() 中,未被覆蓋的部分(兩個矩形)用陰影表示.設左上角與右下角的陰影部分的面積的差為
中,未被覆蓋的部分(兩個矩形)用陰影表示.設左上角與右下角的陰影部分的面積的差為![]() ,當
,當![]() 的長度變化時,按照同樣的放置方式,
的長度變化時,按照同樣的放置方式,![]() 始終保持不變,則
始終保持不變,則![]() ,
,![]() 滿足的關系式為( )
滿足的關系式為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
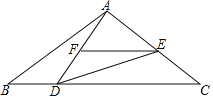
【題目】如圖:已知在△ABC中,AB=AC,點D是BC上一點,∠ADE=∠B,
(1)求證:△ABD~△DCE;
(2)點F在AD上,且![]() =
=![]() ,求證:EF∥CD.
,求證:EF∥CD.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】華星商店準備從陽光機械廠購進甲、乙兩種零件進行銷售,若一個甲種零件的進價比一個乙種零件的進價多50元,用4000元購進甲種零件的數量是用1500元購進乙種零件的數量的2倍.
(1)求每個甲種零件,每個乙種零件的進價分別為多少元?
(2)華星商店甲種零件每件售價為260元,乙種零件每件售價為190元,商店根據市場需求.決定向該廠購進一批零件、且購進乙種零件的數量比購進甲種零件的數量的2倍還多4個,若本次購進的兩種零件全部售出后,總獲利不少于2400元、求該商店本次購進甲種零件至少是多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AD=![]() AB,∠BAD的平分線交BC于點E,DH⊥AE于點H,連接BH并延長交CD于點F,連接DE交BF于點O,下列結論:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正確的有( )
AB,∠BAD的平分線交BC于點E,DH⊥AE于點H,連接BH并延長交CD于點F,連接DE交BF于點O,下列結論:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正確的有( )

A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中 xOy 中,對于⊙C及⊙C內一點 P,給出如下定義:若存在過點 P 的直線 l,使得它與⊙C 相交所截得的弦長為![]() ,則稱點 P 為⊙C的“k-近內點”.
,則稱點 P 為⊙C的“k-近內點”.
(1)已知⊙O的半徑為 4,
①在點中![]() ,⊙O的“4-近內點”是______________;
,⊙O的“4-近內點”是______________;
②點 P 在直線y=![]() x上,若點 P 為⊙O的“4-近內點”,則點 P 的縱坐標y的取值范圍是____________;
x上,若點 P 為⊙O的“4-近內點”,則點 P 的縱坐標y的取值范圍是____________;
(2)⊙C的圓心為(-1,0),半徑為 3,直線![]() x 軸,y 軸分別交于 M,N,若線段 MN 上存在⊙C的 “2
x 軸,y 軸分別交于 M,N,若線段 MN 上存在⊙C的 “2![]() -近內點”,則 b 的取值范圍是____________.
-近內點”,則 b 的取值范圍是____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com