
【題目】若![]() ,則
,則![]() =____.
=____.
【答案】-4或3
【解析】
根據絕對值的幾何意義,可知|x-2|是數軸上表示數x的點與表示數2的點之間的距離,|x+3|是數軸上表示數x的點與表示數-3的點之間的距離,而2與-3之間的距離為5,由|x-2|+|x+3|=7,可以判斷x表示的數在表示數2的點的右邊,或在表示數-3的點的左邊,然后根據兩點間的距離公式計算即可.
∵|x-2|+|x+3|=7,
根據絕對值的幾何意義,可知數x,表示數x的點與表示數2的點之間的距離與表示數-3的點之間的距離之和為7,而2與-3之間的距離為5,
∴表示數x的點的位置有兩個:①在表示數2的點的右邊,即x>2;②在表示數-3的點的左邊,即x<-3.
①當x>2時,
|x-2|+|x+3|=7,
x-2+x+3=7
2x=6
x=3,
②當x<-3時,
|x-2|+|x+3|=7,
2-x-x-3=7,
-2x=8,
x=-4.
故答案為:3或-4.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是菱形,對角線AC與BD交于點O,且AC=80,BD=60.動點M,N分別以每秒1個單位的速度從點A,D同時出發,分別沿A→O→D和D→A運動,當點N到達點A時,M,N同時停止運動.設運動時間為t秒.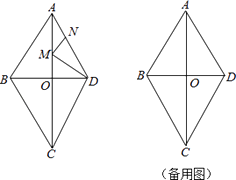
(1)求菱形ABCD的周長.
(2)設△DMN的面積為S,求S關于t的解析式,并求S的最大值(提示:需分兩種情況討論).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀,后解答: ![]() =
= ![]() =
= ![]() =3+
=3+ ![]()
像上述解題過程中, ![]() ﹣
﹣ ![]() 與
與 ![]() +
+ ![]() 相乘,積不含有二次根式,我們可將這兩個式子稱為互為有理化因式,上述解題過程也稱為分母有理化,
相乘,積不含有二次根式,我們可將這兩個式子稱為互為有理化因式,上述解題過程也稱為分母有理化,
(1)![]() 的有理化因式是;
的有理化因式是; ![]() +2的有理化因式是
+2的有理化因式是
(2)將下列式子進行分母有理化: ![]() =;
=; ![]() = .
= .
(3)已知a= ![]() ,b=2﹣
,b=2﹣ ![]() ,比較a與b的大小關系.
,比較a與b的大小關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校運動會需購買A,B兩種獎品,若購買A種獎品3件和B種獎品2件,共需60元;若購買A種獎品5件和B種獎品3件,共需95元.
(1)求A、B兩種獎品的單價各是多少元?
(2)學校計劃購買A、B兩種獎品共100件,購買費用不超過1150元,且A種獎品的數量不大于B種獎品數量的3倍,設購買A種獎品m件,購買費用為W元,寫出W(元)與m(件)之間的函數關系式.求出自變量m的取值范圍,并確定最少費用W的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點A、C分別在x、y軸的正半軸上,點D為對角線OB的中點,點E(4,n)在邊AB上,反比例函數 ![]() (k≠0)在第一象限內的圖像經過點D、E,且tan∠BOA=
(k≠0)在第一象限內的圖像經過點D、E,且tan∠BOA= ![]() .
.
(1)求邊AB的長;
(2)求反比例函數的解析式和n的值;
(3)若反比例函數的圖像與矩形的邊BC交于點F,將矩形折疊,使點O與點F重合,折痕分別與x、y軸正半軸交于點H、G,求線段OG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某高中學校為使高一新生入校后及時穿上合身的校服,現提前對某校九年級(3)班學生即將所穿校服型號情況進行了摸底調查,并根據調查結果繪制了如圖兩個不完整的統計圖(校服型號以身高作為標準,共分為6種型號).
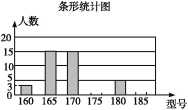
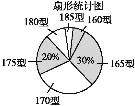
根據以上信息,解答下列問題:
(1)該班共有多少名學生?其中穿175型校服的學生有多少人?
(2)在條形統計圖中,請把空缺的部分補充完整;
(3)在扇形統計圖中,請計算185型校服所對應扇形圓心角的大小;
(4)求該班學生所穿校服型號的眾數和中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了參觀上海世博會,某公司安排甲、乙兩車分別從相距300千米的上海、泰州兩地同時出發相向而行,甲到泰州帶客后立即返回,下圖是它們離各自出發地的距離y(千米)與行駛時間x(小時)之間的函數圖像. 
(1)請直接寫出甲離出發地的距離y(千米)與行駛時間x(小時)之間的函數關系式,并寫出自變量x的取值范圍;
(2)當它們行駛4.5小時后離各自出發點的距離相等,求乙車離出發地的距離y(千米)與行駛時間x(小時)之間的函數關系式,并寫出自變量x的取值范圍;
(3)在(2)的條件下,甲、乙兩車從各自出發地駛出后經過多少時間相遇?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點D、E、F分別在AB、BC、AC邊上,且BE=CF,BD=CE.
(1)求證:△DEF是等腰三角形;
(2)當∠A=40°時,求∠DEF的度數;

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com