【題目】在某班“講故事”比賽中有一個抽獎活動，活動規則是：只有進入最后決賽的甲、乙、丙三位同學，每人才能獲得一次抽獎機會．在如圖所示的翻獎牌正面的4個數字中選一個數字，選中后就可以得到該數字后面的相應獎品：前面的人選中的數字，后面的人就不能再選擇數字了．
（1）請用樹狀圖（或列表）的方法求甲、乙二人得到的獎品都是計算器的概率．
（2）有的同學認為，如果甲先翻獎牌，那么他得到籃球的概率會大些，這種說法正確嗎？請說明理由．
【答案】（1）
；（2）這種說法是不正確的．理由見解析．
【解析】
試題分析：（1）首先畫樹形圖可知：一共有24種情況，甲、乙二人都得到計算器共有2種情況除以總情況數即為所求概率；
（2）根據（1）中的樹形圖，分別求出甲、乙、丙得到籃球的概率即可．
試題解析：（1）所有獲獎情況的樹狀圖如下：
共有24種可能的情況，其中甲、乙二人都得到計算器共有4種情況，
所以，甲、乙二人都得計算器的概率為：P=
；
（2）這種說法是不正確的．由上面的樹狀圖可知共有24種可能情況：
甲得到籃球有六種可能情況：P（甲）=
，
乙得到籃球有六種可能情況：P（乙）=，
丙得到籃球有六種可能情況：P（丙）=，
所以甲、乙、丙三人不管誰先翻獎牌得到籃球的概率都相等．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】如圖，矩形
的頂點A、C分別在
、
的正半軸上，反比例函數
（
）與矩形的邊AB、BC交于點D、E．
（1）若
，則
的面積為_________；
（2）若D為AB邊中點．
①求證：E為BC邊中點；
②若
的面積為4，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，AB=5cm，∠ADC=120°，點E、F同時由A、C兩點出發，分別沿AB．CB方向向點B勻速移動(到點B為止)，點E的速度為1cm/s，點F的速度為2cm/s，經過t秒△DEF為等邊三角形，則t的值為( )
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把下列各數填在相應的大括號里：
1，﹣
，8.9，﹣7， 
，﹣3.2，+1 008，﹣0.06，28，﹣9．
正整數集合：{______…}；
負整數集合：{______…}；
正分數集合：{______…}；
負分數集合：{______…}．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一家商店準備進行裝修，若請甲、乙兩個裝修隊同時施工，8天完成，需付兩隊共3520元費用；若先請甲隊單獨做6天，再請乙隊單獨做12天可以完成，需付兩隊共3480元費用。
(1)甲、乙兩隊工作一天，商場各應付多少元?
(2)單獨請哪個隊裝修，商場所付費用最少?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某工廠計劃在規定時間內生產24000個零件．由于銷售商突然急需供貨，工廠實際工作效率比原計劃提高了50%，并提前5天完成這批零件的生產任務．求該工廠原計劃每天加工這種零件多少個？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】探究題：已知：如圖,
,
.求證：
.
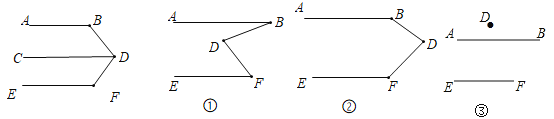
老師要求學生在完成這道教材上的題目證明后，嘗試對圖形進行變形，繼續做拓展探究，看看有什么新發現？
（1）小穎首先完成了對這道題的證明，在證明過程中她用到了平行線的一條性質，小穎用到的平行線性質可能是 .
（2）接下來，小穎用《幾何畫板》對圖形進行了變式，她先畫了兩條平行線
，然后在平行線間畫了一點
，連接
后，用鼠標拖動點，分別得到了圖
，小穎發現圖
正是上面題目的原型，于是她由上題的結論猜想到圖和
圖中的與
之間也可能存在著某種數量關系.于是她利用《幾何畫板》的度量與計算功能，找到了這三個角之間的數量關系.
請你在小穎操作探究的基礎上，繼續完成下面的問題：
（ⅰ）猜想圖中與
之間的數量關系并加以證明；
（ⅱ）補全圖，直接寫出與之間的數量關系： .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，在△ABC中，∠ABC與∠ACB的平分線相交于點P．
（1）如果∠A=80°，求∠BPC的度數；
（2）如圖②，作△ABC外角∠MBC，∠NCB的角平分線交于點Q，試探索∠Q、∠A之間的數量關系．
（3）如圖③，延長線段BP、QC交于點E，△BQE中，存在一個內角等于另一個內角的2倍，求∠A的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
