
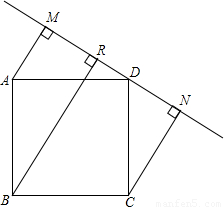
 (1)證明:∵AM⊥MN于點M,CN⊥MN于點N(已知),
(1)證明:∵AM⊥MN于點M,CN⊥MN于點N(已知),

科目:初中數(shù)學 來源: 題型:
| ||
| 3 |
| ||
| 3 |
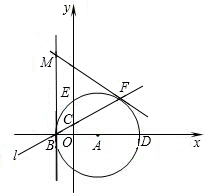 (1)直接寫出點B、C的坐標;
(1)直接寫出點B、C的坐標; |
| BEF |
 |
| BEF |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
查看答案和解析>>
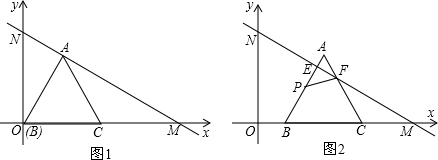
科目:初中數(shù)學 來源:2004年全國中考數(shù)學試題匯編《一次函數(shù)》(04)(解析版) 題型:解答題
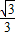 x+
x+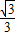 與x軸、y軸分別交于點B、C,以點A(1,0)為圓心,以AB的長為半徑作⊙A,分別交x軸、y軸正半軸于點D、E,直線l與⊙A交于點F,分別過點B、F作⊙A的切線交于點M.
與x軸、y軸分別交于點B、C,以點A(1,0)為圓心,以AB的長為半徑作⊙A,分別交x軸、y軸正半軸于點D、E,直線l與⊙A交于點F,分別過點B、F作⊙A的切線交于點M.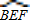 上任意一點(不與B、F重合).連接BP、FP.過點M作MN∥PF,交直線l于點N.設(shè)PB=a,MN=b,求b與a的函數(shù)關(guān)系式,并寫出自變量a的取值范圍;
上任意一點(不與B、F重合).連接BP、FP.過點M作MN∥PF,交直線l于點N.設(shè)PB=a,MN=b,求b與a的函數(shù)關(guān)系式,并寫出自變量a的取值范圍;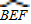 上任意一點,改為點P是⊙A上任意一點,其它條件不變.當點P在⊙A上的什么位置時,△BMN為直角三角形,并寫出此時點N的坐標.(第(4)問直接寫出結(jié)果,不要求證明或計算過程)
上任意一點,改為點P是⊙A上任意一點,其它條件不變.當點P在⊙A上的什么位置時,△BMN為直角三角形,并寫出此時點N的坐標.(第(4)問直接寫出結(jié)果,不要求證明或計算過程)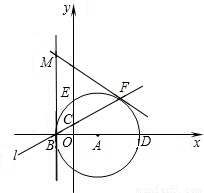
查看答案和解析>>
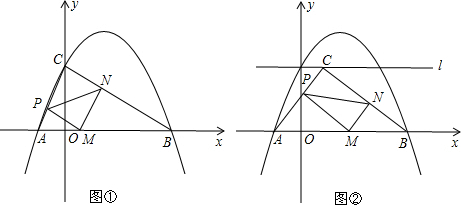
科目:初中數(shù)學 來源:2004年遼寧省沈陽市中考數(shù)學試卷(解析版) 題型:解答題
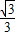 x+
x+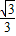 與x軸、y軸分別交于點B、C,以點A(1,0)為圓心,以AB的長為半徑作⊙A,分別交x軸、y軸正半軸于點D、E,直線l與⊙A交于點F,分別過點B、F作⊙A的切線交于點M.
與x軸、y軸分別交于點B、C,以點A(1,0)為圓心,以AB的長為半徑作⊙A,分別交x軸、y軸正半軸于點D、E,直線l與⊙A交于點F,分別過點B、F作⊙A的切線交于點M.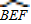 上任意一點(不與B、F重合).連接BP、FP.過點M作MN∥PF,交直線l于點N.設(shè)PB=a,MN=b,求b與a的函數(shù)關(guān)系式,并寫出自變量a的取值范圍;
上任意一點(不與B、F重合).連接BP、FP.過點M作MN∥PF,交直線l于點N.設(shè)PB=a,MN=b,求b與a的函數(shù)關(guān)系式,并寫出自變量a的取值范圍;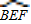 上任意一點,改為點P是⊙A上任意一點,其它條件不變.當點P在⊙A上的什么位置時,△BMN為直角三角形,并寫出此時點N的坐標.(第(4)問直接寫出結(jié)果,不要求證明或計算過程)
上任意一點,改為點P是⊙A上任意一點,其它條件不變.當點P在⊙A上的什么位置時,△BMN為直角三角形,并寫出此時點N的坐標.(第(4)問直接寫出結(jié)果,不要求證明或計算過程)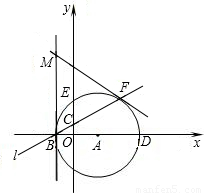
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com