
【題目】如圖,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,連接BE、AD,P為BD中點,M為AB中點、N為DE中點,連接PM、PN、MN.
(1)試判斷△PMN的形狀,并證明你的結論;
(2)若CD=5,AC=12,求△PMN的周長.
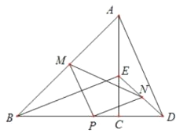
【答案】(1)△PMN為等腰直角三角形. 見詳解 (2)13+![]() .
.
【解析】
(1) 由等腰Rt△ABC和△CDE證得△BCE≌△ACD,由M,N,P分別為AB,DE,BD的中點,得PN∥BE,PN=![]() BE,PM∥AD,PM=
BE,PM∥AD,PM=![]() AD,證得△PMN為等腰三角形,再由∠BPM=∠BDA且∠BDA+∠DAC=90°,所以∠BPM+∠EBP=90°,所以∠BFP=90°,再根據平行的性質即可求解.
AD,證得△PMN為等腰三角形,再由∠BPM=∠BDA且∠BDA+∠DAC=90°,所以∠BPM+∠EBP=90°,所以∠BFP=90°,再根據平行的性質即可求解.
(2) 因為Rt△ACD,所以根據勾股定理求得AD,再因為PM=![]() AD,求得PM=PN=
AD,求得PM=PN=![]() ,再根據求得的△PMN為等腰直角三角形,勾股定理求得MN,最后相加即可求解.
,再根據求得的△PMN為等腰直角三角形,勾股定理求得MN,最后相加即可求解.
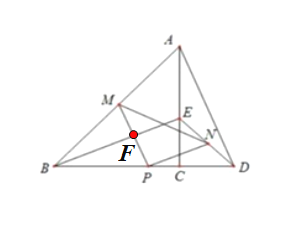
(1)△PMN為等腰直角三角形.
證明:在等腰Rt△ABC和等腰Rt△ECD中,AC=BC,CD=CE,易得△BCE≌△ACD.
∴BE=AD,∠CBE=∠DAC.
又∵M,N,P分別為AB,DE,BD的中點,
∴PN∥BE,PN=![]() BE,PM∥AD,PM=
BE,PM∥AD,PM=![]() AD.
AD.
又∵BE=AD,
∴PM=PN.
又∵PM∥AD,
∴∠BPM=∠BDA且∠BDA+∠DAC=90°,
∴∠BPM+∠EBP=90°,
∴∠BFP=90°.
又∵BE∥PN,
∴∠FPN=90°.
∴△PMN為等腰直角三角形.
(2)在Rt△ACD中,CD=5,AC=12,由勾股定理得
AD=13,
∴PM=PN=![]() ,MN=
,MN=![]() ,
,
∴C△PMN=![]() +
+![]() +
+![]() =13+
=13+![]() .
.


科目:初中數學 來源: 題型:
【題目】為了響應市委和市政府“綠色環保,節能減排”的號召,幸福商場用3300元購進甲、乙兩種節能燈共計100只,很快售完.這兩種節能燈的進價、售價如下表:
進價(元/只) | 售價(元/只) | |
甲種節能燈 | 30 | 40 |
甲種節能燈 | 35 | 50 |
(1)求幸福商場甲、乙兩種節能燈各購進了多少只?
(2)全部售完100只節能燈后,商場共計獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線C1:y=﹣x2+2mx+1(m為常數,且m≠0)的頂點為A,與y軸交于點C;拋物線C2與拋物線C1關于y軸對稱,其頂點為B.若點P是拋物線C1上的點,使得以A、B、C、P為頂點的四邊形為菱形,則m為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現在,蘇寧商場進行促銷活動,出售一種優惠購物卡(注:此卡只作為購物優惠憑證不能頂替貨款),花300元買這種卡后,憑卡可在這家商場按標價的8折購物.
(1)顧客購買多少元金額的商品時,買卡與不買卡花錢相等?在什么情況下購物合算?
(2)小張要買一臺標價為3500元的冰箱,如何購買合算?小張能節省多少元錢?
(3)小張按合算的方案,把這臺冰箱買下,如果商場還能盈利25%,這臺冰箱的進價是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】擲一枚正方體的骰子,各個面上分別標有數字1,2,3,4,5,6,求下列事件發生的頻率的大小:
①朝上的數字是奇數;
②朝上的數字能被3除余1;
③朝上的數字小于6;
④朝上的數字不小于3.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形廣告牌架在樓房頂部,已知CD=2m,經測量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的長.(參考數據:tan37°≈0.75, ![]() ≈1.732,結果精確到0.1m)
≈1.732,結果精確到0.1m) 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() .
.
(1)找出圖中相等的銳角,并說明理由.
(2)求出點![]() 到直線
到直線![]() 的距離以及點
的距離以及點![]() 到直線
到直線![]() 的距離.
的距離.
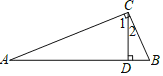
解:(1)![]() (已知),
(已知),
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() .
.
同理可證,
![]() .
.
(2)點![]() 到直線
到直線![]() 的距離
的距離![]()
![]() .
.
![]() 到直線
到直線![]() 的距離為線段 的長度.
的距離為線段 的長度.
![]()
![]()
![]()
![]() (填線段名稱).
(填線段名稱).
![]() ,
,![]() ,
,![]() ,代入上式,解得
,代入上式,解得
![]()
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com