



 ,
,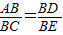 .
. .
. ,∵
,∵ ,
, .(5分)
.(5分)

科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源:北京期末題 題型:解答題

 ,∠BDE=
,∠BDE= ,在繞點B旋轉的過程中,直線AD與EC夾角的度數是否改變?若不改變,直接用含
,在繞點B旋轉的過程中,直線AD與EC夾角的度數是否改變?若不改變,直接用含 、
、 的式子表示夾角的度數;若改變,請說明理由。
的式子表示夾角的度數;若改變,請說明理由。查看答案和解析>>
科目:初中數學 來源:2010-2011學年北京市昌平區九年級(上)期末數學試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com