
 如圖,已知點A(0,2),B(2,2),C(-1,-2),拋物線F:y=(x-m)2-2與直線x=-2交于點P.
如圖,已知點A(0,2),B(2,2),C(-1,-2),拋物線F:y=(x-m)2-2與直線x=-2交于點P.分析 (1)根據(jù)拋物線F:y=(x-m)2-2過點C(-1,-2),可以求得拋物線F的表達式;
(2)根據(jù)題意,可以求得yP的最小值和此時拋物線的表達式,從而可以比較y1與y2的大小;
(3)根據(jù)題意可以列出相應(yīng)的不等式組,從而可以解答本題.
解答 解:(1)∵拋物線F經(jīng)過點C(-1,-2),
∴-2=(-1)2-2×m×(-1)+m2-2,
解得,m=-1,
∴拋物線F的表達式是:y=x2+2x-1;
(2)當(dāng)x=-2時,yp=4+4m+m2-2=(m+2)2-2,
∴當(dāng)m=-2時,yp的最小值-2,
此時拋物線F的表達式是:y=x2+4x+2=(x+2)2-2,
∴當(dāng)x≤-2時,y隨x的增大而減小,
∵x1<x2≤-2,
∴y1>y2;
(3)m的取值范圍是-2≤m≤0或2≤m≤4,
理由:∵拋物線F與線段AB有公共點,點A(0,2),B(2,2),
∴$\left\{\begin{array}{l}{{m}^{2}-2≤2}\\{{2}^{2}-2m×2+{m}^{2}-2≥2}\end{array}\right.$或$\left\{\begin{array}{l}{{m}^{2}-2≥2}\\{{2}^{2}-2m×2+{m}^{2}-2≤2}\end{array}\right.$,
解得:-2≤m≤0或2≤m≤4.
故答案為:-2≤m≤0或2≤m≤4.
點評 本題考查二次函數(shù)的性質(zhì)、二次函數(shù)圖象上點的坐標特征、待定系數(shù)法求二次函數(shù)解析式,解題的關(guān)鍵是明確題意,找出所求問題需要的條件,利用數(shù)形結(jié)合的思想解答問題.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 個 | B. | 2 個 | C. | 3 個 | D. | 4 個 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 在每一象限內(nèi),y隨x的增大而增大 | B. | 在每一象限內(nèi),y隨x的增大而減小 | ||
| C. | y恒為正值 | D. | y恒為負值 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,已知A(-4,-$\frac{1}{2}$),B(-1,-2)是一次函數(shù)y=kx+b與反比例函數(shù)y=$\frac{m}{x}$(m>0,x<0)圖象的兩個交點,AC⊥x軸于C,BD⊥y軸于D.
如圖,已知A(-4,-$\frac{1}{2}$),B(-1,-2)是一次函數(shù)y=kx+b與反比例函數(shù)y=$\frac{m}{x}$(m>0,x<0)圖象的兩個交點,AC⊥x軸于C,BD⊥y軸于D.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
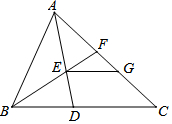 如圖,△ABC中,∠BAC=∠ADB,BE平分∠ABC交AD于點E,交AC于點F,過點E作EG∥BC交AC于點G.
如圖,△ABC中,∠BAC=∠ADB,BE平分∠ABC交AD于點E,交AC于點F,過點E作EG∥BC交AC于點G.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,已知:?ABCD的對角線AC,BD相交于點O,EF過O,AD=8,AB=6,OE=4,則四邊形ABFE的周長是多少?
如圖,已知:?ABCD的對角線AC,BD相交于點O,EF過O,AD=8,AB=6,OE=4,則四邊形ABFE的周長是多少?查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com