Question

如圖，在正方形ABCD中，對角線AC與BD相交于點O，點E是BC上的一個動點，連接DE，交AC于點F．

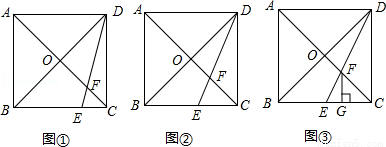
（1）如圖①，當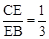時，求的值；

（2）如圖②當DE平分∠CDB時，求證：AF=OA；

（3）如圖③，當點E是BC的中點時，過點F作FG⊥BC于點G，求證：CG=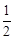BG．

 

Answer 1

【答案】

解：（1）∵，∴。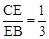

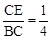∵四邊形ABCD是正方形，∴AD∥BC，AD=BC。∴△CEF∽△ADF。

∴。∴。∴。

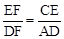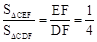（2）證明：∵DE平分∠CDB，∴∠ODF=∠CDF。

又∵AC、BD是正方形ABCD的對角線．∴∠ADO=∠FCD=45°，∠AOD=90°，OA=OD。

又∵∠ADF=∠ADO+∠ODF，∠AFD=∠FCD+∠CDF，∴∠ADF=∠AFD。∴AD=AF。

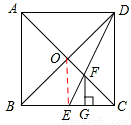
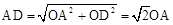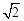在Rt△AOD中，根據勾股定理得：，∴AF=OA。

（3）證明：連接OE，

∵點O是正方形ABCD的對角線AC、BD的交點，

∴點O是BD的中點。

又∵點E是BC的中點，∴OE是△BCD的中位線。

∴OE∥CD，OE=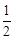CD。∴△OFE∽△CFD。

∴。∴。

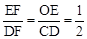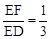又∵FG⊥BC，CD⊥BC，∴FG∥CD。∴△EGF∽△ECD。∴。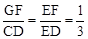

在Rt△FGC中，∵∠GCF=45°，∴CG=GF。

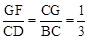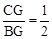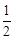又∵CD=BC，∴。∴。∴CG=BG。

【解析】

試題分析：（1）利用相似三角形的性質求得EF于DF的比值，依據△CEF和△CDF同高，則面積的比就是EF與DF的比值，據此即可求解。

（2）利用角之間的關系到證得∠ADF=∠AFD，可以證得AD=AF，在Rt△AOD中，利用勾股定理可以證得。

（3）連接OE，易證OE是△BCD的中位線，然后根據△FGC是等腰直角三角形，易證△EGF∽△ECD，利用相似三角形的對應邊的比相等即可證得。