
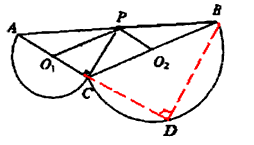
 上分別取點E、F,使∠AO1E=∠BO2F,則有結(jié)論①△PO1E≌△FO2P,②四邊形PO1CO2是菱形,請給出結(jié)論②的證明;
上分別取點E、F,使∠AO1E=∠BO2F,則有結(jié)論①△PO1E≌△FO2P,②四邊形PO1CO2是菱形,請給出結(jié)論②的證明;
| 解:(1)∵P、O1、O2分別為AB、AC、BC的中點, ∴AP=BP,AO1=BO2, 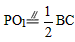 , ,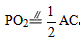 , ,∴四邊形PO1CO2是平行四邊形, ∵AC=BC, ∴PO1=PO2, ∴四邊形PO1CO2是菱形; |
|
| (2)結(jié)論①成立,結(jié)論②不成立, 結(jié)論①證明如下: ∵P、O1、O2分別為AB、AC、BC的中點, ∴AP=BP,AO1=BO2, 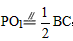 , ,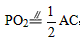 , ,即PO1=BO2,AO1=PO2, ∴△APO1≌△BPO2(SSS); |
|
| (3)直角三角形APC中,設AP=c,AC=a,PC=b, ∴ 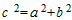 ; ;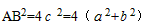 , ,過點B作AC的垂線,交AC的延長線于D點, ∵PC⊥AD,BD⊥AD, ∴PC∥BD, 又∵AP=BP, ∴CD=a,BD=2b,BC2=2a2+4b2, ∴  , ,∴AB2=BC2+3AC2。 |
 |


科目:初中數(shù)學 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:


查看答案和解析>>
科目:初中數(shù)學 來源: 題型:


查看答案和解析>>
科目:初中數(shù)學 來源: 題型:閱讀理解

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:閱讀理解

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com