
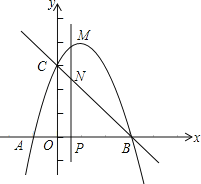
【題目】如圖,拋物線y=﹣x2+bx+c與x軸交于A(﹣1,0),B兩點(點A在點B的左側),與y軸交于點C(0,3),作直線BC.動點P在x軸上運動,過點P作PM⊥x軸,交拋物線于點M,交直線BC于點N,設點P的橫坐標為m.
(1)求拋物線的解析式;
(2)當點P在線段OB上運動時,求線段MN的最大值;
(3)是否存在點P,使得以點C、O、M、N為頂點的四邊形是平行四邊形?若存在,請直接寫出m的值;若不存在,請說明理由.
【答案】(1)y=﹣x2+2x+3;(2)線段MN最大值為![]() ;(3)存在點P,使得以點C、O、M、N為頂點的四邊形是平行四邊形,此時m的值為
;(3)存在點P,使得以點C、O、M、N為頂點的四邊形是平行四邊形,此時m的值為![]() 或
或![]() .
.
【解析】
(1)根據點A、C的坐標,利用待定系數法即可求出拋物線的解析式;
(2)由二次函數圖象上點的坐標特征可找出點B的坐標,根據點B、C的坐標,利用待定系數法可求出直線BC的解析式,設點P的坐標為(m,0)(0≤m≤3),點M的坐標為(m,﹣m2+2m+3),點N的坐標為(m,﹣m+3),由此即可得出MN=﹣m2+3m,利用配方法即可求出線段MN的最大值;
(3)根據平行四邊形的性質可得出MN=OC,分m<0或m>3以及0≤m≤3兩種情況,即可得出關于m的一元二次方程,解之即可得出結論.
(1)將A(﹣1,0)、C(0,3)代入y=﹣x2+bx+c中,
![]() ,解得:
,解得:![]() ,
,
∴拋物線的解析式為y=﹣x2+2x+3.
(2)當y=﹣x2+2x+3=0時,x1=﹣1,x2=3,
∴點B的坐標為(3,0).
設直線BC的解析式為y=kx+b(k≠0),
將B(3,0)、C(0,3)代入y=kx+b中,
![]() ,,解得:
,,解得:![]() ,
,
∴直線BC的解析式為y=﹣x+3.
設點P的坐標為(m,0)(0≤m≤3),點M的坐標為(m,﹣m2+2m+3),
點N的坐標為(m,﹣m+3),
∴MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣![]() )2+
)2+![]() ,
,
∴當m=![]() ,線段MN取最大值,最大值為
,線段MN取最大值,最大值為![]() .
.
(3)∵MN∥CO,
∴當MN=CO時,以點C、O、M、N為頂點的四邊形是平行四邊形.
∵點O(0,0)、C(0,3),
∴OC=3,
∴|﹣m2+3m|=3,
當m<0或m>3時,有m2﹣3m=3,
解得:m1=![]() ,m2=
,m2=![]() ;
;
當0≤m≤3時,有﹣m2+3m=3,
∵△=(﹣3)2﹣4×1×3=﹣3<0,
∴此時方程無解.
綜上所述:存在點P,使得以點C、O、M、N為頂點的四邊形是平行四邊形,此時m的值為![]() 或
或![]() .
.


 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:初中數學 來源: 題型:
【題目】綜合與實踐
問題情境
數學活動課上,老師讓同學們以“三角形的旋轉”為主題開展數學活動,![]() 和
和![]() 是兩個全等的直角三角形紙片,其中
是兩個全等的直角三角形紙片,其中![]() ,
,![]() ,
,![]() .
.
解決問題
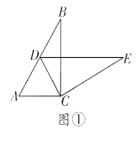
(1)如圖①,智慧小組將![]() 繞點
繞點![]() 順時針旋轉,發現當點
順時針旋轉,發現當點![]() 恰好落在
恰好落在![]() 邊上時,
邊上時,![]() ,請你幫他們證明這個結論;
,請你幫他們證明這個結論;
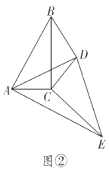
(2)縝密小組在智慧小組的基礎上繼續探究,連接![]() ,當
,當![]() C繞點
C繞點![]() 繼續旋轉到如圖②所示的位置時,他們提出
繼續旋轉到如圖②所示的位置時,他們提出![]() ,請你幫他們驗證這一結論是否正確,并說明理由;
,請你幫他們驗證這一結論是否正確,并說明理由;
探索發現
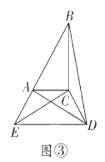
(3)如圖③,勤奮小組在前兩個小組的啟發下,繼續旋轉![]() ,當
,當![]() 三點共線時,求
三點共線時,求![]() 的長;
的長;
(4)在圖①的基礎上,寫出一個邊長比為![]() 的三角形(可添加字母).
的三角形(可添加字母).
查看答案和解析>>
科目:初中數學 來源: 題型:
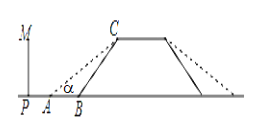
【題目】某地的一座人行天橋如圖所示,天橋高為6米,坡面BC的坡度為1:1,為了方便行人推車過天橋,有關部門決定降低坡度,使新坡面的坡度為1:![]() .
.
(1)求新坡面的坡角∠CAB的度數;
(2)原天橋底部正前方8米處(PB的長)的文化墻PM是否需要拆除?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】河南省開封市鐵塔始建于公元1049年(北宋皇祐元年),是國家重點保護文物之一,在900多年中,歷經了數次地震、大風、水患而巍然屹立,素有“天下第一塔”之稱.如圖,小明在鐵塔一側的水平面上一個臺階的底部A處測得塔頂P的仰角為45°,走到臺階頂部B處,又測得塔頂P的仰角為38.7°,已知臺階的總高度BC為3米,總長度AC為10米,試求鐵塔的高度.(結果精確到1米,參考數據:sin38.7°≈0.63,cos38.7°≈0.78,tan38.7°≈0.80)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為弘揚泰山文化,某校舉辦了“泰山詩文大賽”活動,從中隨機抽取部分學生的比賽成績,根據成績(成績都高于50分),繪制了如下的統計圖表(不完整):
組別 | 分數 | 人數 |
第1組 | 90<x≤100 | 8 |
第2組 | 80<x≤90 | a |
第3組 | 70<x≤80 | 10 |
第4組 | 60<x≤70 | b |
第5組 | 50<x≤60 | 3 |
請根據以上信息,解答下列問題:

(1)求出a,b的值;
(2)計算扇形統計圖中“第5組”所在扇形圓心角的度數;
(3)若該校共有1800名學生,那么成績高于80分的共有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在抗擊“新冠肺炎”戰役中,某公司接到轉產生產1440萬個醫用防護口罩補充防疫一線需要的任務,臨時改造了甲、乙兩條流水生產線.試產時甲生產線每天的產能(每天的生產的數量)是乙生產線的2倍,各生產80萬個,甲比乙少用了2天.
(1)求甲、乙兩條生產線每天的產能各是多少?
(2)若甲、乙兩條生產線每天的運行成本分別是1.2萬元和0.5萬元,要使完成這批任務總運行成本不超過40萬元,則至少應安排乙生產線生產多少天?
(3)正式開工滿負荷生產3天后,通過技術革新,甲生產線的日產能提高了50%,乙生產線的日產能翻了一番.再滿負荷生產13天能否完成任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數y=kx+4與二次函數y=ax2+c的圖像的一個交點坐標為(1,2),另一個交點是該二次函數圖像的頂點
(1)求k,a,c的值;
(2)過點A(0,m)(0<m<4)且垂直于y軸的直線與二次函數y=ax2+c的圖像相交于B,C兩點,點O為坐標原點,記W=OA2+BC2,求W關于m的函數解析式,并求W的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
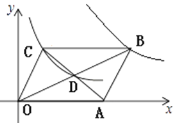
【題目】如圖,在平面直角坐標系中,平行四邊形OABC的對角線交于點D.雙曲線![]() 經過C,D 兩點,雙曲線
經過C,D 兩點,雙曲線![]() 經過點B,則平行四邊形OABC的面積為( )
經過點B,則平行四邊形OABC的面積為( )
A.4B.6C.7D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“六一”期間,小張購進100只兩種型號的文具進行銷售,其進價和售價之間的關系如下表:
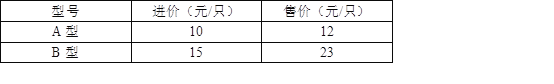
(1)小張如何進貨,使進貨款恰好為1300元?
(2)要使銷售文具所獲利潤最大,且所獲利潤不超過進貨價格的40%,請你幫小張設計一個進貨方案,并求出其所獲利潤的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com