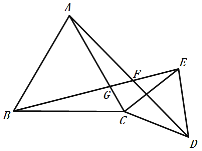
【題目】如圖，△ABC和△CDE都是等邊三角形，連接AD、BE，AD與BE交于點F．
（1）求證AD＝BE；
（2）∠BFA＝ °．
【答案】（1）證明見解析；（2）60.
【解析】
（1）△ABC和△CDE都是等邊三角形，根據等邊三角形的性質，利用SAS可證得△ACD≌△BCE，從而證得結果；
（2）在
和
中，利用（1）的結論結合對頂角相等，可求得答案.
（1）∵△ABC和△CDE都是等邊三角形，
∴AC＝BC， CD＝CE，∠ACB＝∠ECD＝60°．
∴∠ACB＋∠ACE＝∠ECD＋∠ACE， 即∠ACD＝∠BCE．
在△ACD和△BCE中，
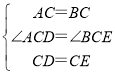
∴△ACD≌△BCE(SAS)．
∴AD＝BE．
（2）∵△ACD≌△BCE
∴∠CAD＝∠CBE
在和中，
∠GAF＝∠GBC
∠AGF＝∠BGC(對頂角相等)
∴∠BFA＝∠ACB＝60
故答案為：60．
科目：初中數學 來源： 題型：
【題目】如圖①、②、③，正三角形
、正方形
、正五邊形
分別是
的內接三角形、內接四邊形、內接五邊形，點
、
分別從點
、
開始，以相同的速度中上逆時針運動．如圖①、②、③，正三角形、正方形、正五邊形分別是的內接三角形、內接四邊形、內接五邊形，點、分別從點、開始，以相同的速度中上逆時針運動．
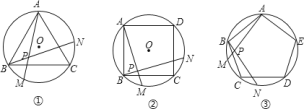
（1）求圖①中
的度數；
（2）圖②中，的度數是________，圖③中的度數是________；
（3）根據前面探索，你能否將本題推廣到一般的正
邊形情況？若能，寫出推廣問題和結論；若不能，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“古圣先賢孝為宗，萬善之門孝為基，禮敬尊親如活佛，成就生命大意義，父母恩德重如山，知恩報恩不忘本，做人飲水要思源，才不愧對父母恩…”.某實驗中學為加強對學生的感恩教育，教學生唱《跪羊圖》，并對學生的學習成果進行隨機抽查，現對部分學生的成績（x為整數，滿分100分）進行了統計，繪制了如下尚不完整的統計圖表.
組別 | 成績分組 （單位：分） | 頻數 | 頻率 |
A |
| 40 | 0.1 |
B |
| 60 | c |
C |
| a | 0.2 |
D |
| 160 | 0.4 |
E |
| 60 | 0.15 |
合計 | b | 1 |
調查結果扇形統計圖
根據以上信息解答下列問題：/p>
（1）統計表中
________，
________，
________；
（2）求扇形統計圖中D組所在扇形的圓心角的度數；
（3）若參加《跪羊圖》演唱的同學共有2000人，請估計成績在90分及以上的學生有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場進行促銷，購物滿額即可獲得1次抽獎機會，抽獎袋中裝有紅色、黃色、白色三種除顏色外都相同的小球，從袋子中摸出1個球，紅色、黃色、白色分別代表一、二、三等獎．
（1）若小明獲得1次抽獎機會，小明中獎是______事件；（填隨機、必然、不可能）
（2）小明觀察一段時間后發現，平均每6個人中會有1人抽中一等獎、2人抽中二等獎，若袋中共有18個球，請你估算袋中白球的數量；
（3）在（2）的條件下，如果在抽獎袋中增加3個黃球，那么抽中一等獎的概率會怎樣變化？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
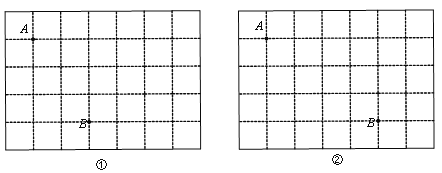
【題目】如圖①、圖②，方格紙中的每個小正方形的邊長均為1，小正方形的頂點稱為格點，圖①和圖②中的點A、點B都是格點．分別在圖①、圖②中畫出格點C，并滿足下面的條件：
（1）在圖①中，使∠ABC＝90°．此時AC的長度是 ．
（2）在圖②中，使AB＝AC．此時△ABC的邊AB上的高是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P是正方形ABCD的對角線BD上一點(點P不與點B、D重合)，PE⊥BC于點E，PF⊥CD于點F，連接EF給出下列五個結論：①AP＝EF；②AP⊥EF；③僅有當∠DAP＝45°或67.5°時，△APD是等腰三角形；④∠PFE＝∠BAP：⑤
PD＝EC．其中有正確有( )個．
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】情境觀察：
如圖1，△ABC中，AB=AC，∠BAC=45°，CD⊥AB，AE⊥BC，垂足分別為D、E，CD與AE交于點F．
①寫出圖1中所有的全等三角形 ；
②線段AF與線段CE的數量關系是 ．
問題探究：
如圖2，△ABC中，∠BAC=45°，AB=BC，AD平分∠BAC，AD⊥CD，垂足為D，AD與BC交于點E．
求證：AE=2CD．
拓展延伸：
如圖3，△ABC中，∠BAC=45°，AB=BC，點D在AC上，∠EDC=
∠BAC，DE⊥CE，垂足為E，DE與BC交于點F．求證：DF=2CE．
要求：請你寫出輔助線的作法，并在圖3中畫出輔助線，不需要證明．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
