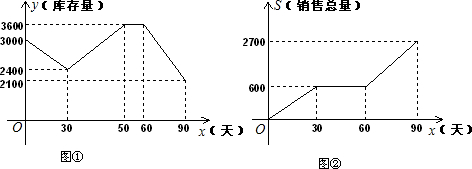
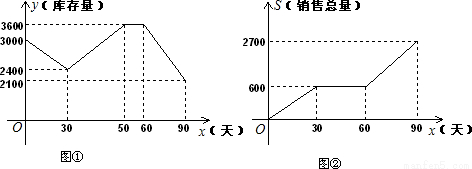
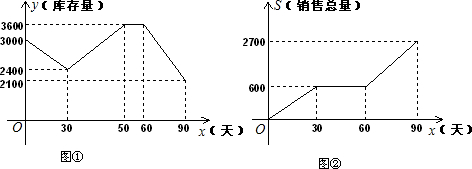
解:(1)根據圖②得出前30天的銷量為600件,故前30天平均每天的銷量是:600÷30=20(件);
(2)當30≤x≤50時,
圖象過(30,2400)和(50,3600)點,
代入y=kx+b,得:
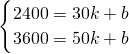
,
解得:

,
則y=60x+600,
當50<x≤60時,
y=3600,
當60<x≤90時,
圖象過(90,2100)和(60,3600)點,
代入y=ax+c,得:
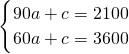
,
解得:
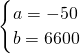
,
則y=-50x+6600;
(3)利用圖①得出當60<x≤90時,庫存量由3600件到2100件,實際減少1500件,
利用圖②得出當60<x≤90時,銷售總量為:2700-600=2100(件),
故當60<x≤90時,實際生產2100-1500=600(件),
則當60<x≤90時,平均每天的生產量為:600÷30=20(件);
(4)按照第60至90天的銷售趨勢,當x=120時,銷售總量為:2100(件),
∵當x=120時,y達到900件,實際減少:2100-900=1200件,
∴90至120天這30天實際生產2100-1200=900(件).
故90至120天這30天平均每天的生產量為:900÷30=30件.
分析:(1)根據圖②解答得出前30天平均每天的銷量即可;
(2)根據圖①知分三段,利用待定系數法分別求解析式;
(3)利用圖①得出當60<x≤90時,庫存量由3600件到2100件,實際減少1500件,利用圖②得出當60<x≤90時,銷售總量為:2700-600=2100(件),
得出實際生產600(件),即可得出平均每天的生產量;
(4)根據當x=120時,銷售總量為:2100(件),利用y達到900件,實際減少:2100-900=1200件,得出90至120天這30天實際生產件數,即可得出平均每天的生產量.
點評:此題主要考查了一次函數的應用以及待定系數法求一次函數解析式,根據已知利用分段函數得出是解決此題的易錯點.

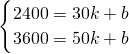 ,
, ,
,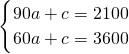 ,
,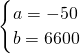 ,
,

 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案