
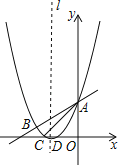
【題目】如圖,拋物線y=![]() x2+bx+c與直線y=
x2+bx+c與直線y=![]() x+3交于A,B兩點,交x軸于C、D兩點,連接AC、BC,已知A(0,3),C(﹣3,0).
x+3交于A,B兩點,交x軸于C、D兩點,連接AC、BC,已知A(0,3),C(﹣3,0).
(1)求拋物線的解析式;
(2)在拋物線對稱軸l上找一點M,使|MB﹣MD|的值最大,并求出這個最大值;
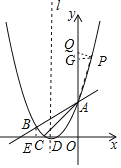
(3)點P為y軸右側拋物線上一動點,連接PA,過點P作PQ⊥PA交y軸于點Q,問:是否存在點P使得以A,P,Q為頂點的三角形與△ABC相似?若存在,請求出所有符合條件的點P的坐標;若不存在,請說明理由.
【答案】(1)拋物線的解析式是y=![]() x2+
x2+![]() x+3;(2)|MB﹣MD|取最大值為
x+3;(2)|MB﹣MD|取最大值為![]() ;(3)存在點P(1,6).
;(3)存在點P(1,6).
【解析】(1)根據待定系數法,可得函數解析式;
(2)根據對稱性,可得MC=MD,根據解方程組,可得B點坐標,根據兩邊之差小于第三邊,可得B,C,M共線,根據勾股定理,可得答案;
(3)根據等腰直角三角形的判定,可得∠BCE,∠ACO,根據相似三角形的判定與性質,可得關于x的方程,根據解方程,可得x,根據自變量與函數值的對應關系,可得答案.
(1)將A(0,3),C(﹣3,0)代入函數解析式,得
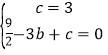 ,解得
,解得![]() ,
,
拋物線的解析式是y=![]() x2+
x2+![]() x+3;
x+3;
(2)由拋物線的對稱性可知,點D與點C關于對稱軸對稱,
∴對l上任意一點有MD=MC,
聯立方程組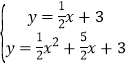 ,
,
解得![]() (不符合題意,舍),
(不符合題意,舍),![]() ,
,
∴B(﹣4,1),
當點B,C,M共線時,|MB﹣MD|取最大值,即為BC的長,
過點B作BE⊥x軸于點E,
 ,
,
在Rt△BEC中,由勾股定理,得
BC=![]() ,
,
|MB﹣MD|取最大值為![]() ;
;
(3)存在點P使得以A,P,Q為頂點的三角形與△ABC相似,
在Rt△BEC中,∵BE=CE=1,
∴∠BCE=45°,
在Rt△ACO中,
∵AO=CO=3,
∴∠ACO=45°,
∴∠ACB=180°﹣45°﹣45°=90°,
過點P作PQ⊥y軸于Q點,∠PQA=90°,
設P點坐標為(x,![]() x2+
x2+![]() x+3)(x>0)
x+3)(x>0)
①當∠PAQ=∠BAC時,△PAQ∽△CAB,
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,
∴△PGA∽△BCA,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
解得x1=1,x2=0(舍去),
∴P點的縱坐標為![]() ×12+
×12+![]() ×1+3=6,
×1+3=6,
∴P(1,6),
②當∠PAQ=∠ABC時,△PAQ∽△CBA,
∵∠PGA=∠ACB=90°,∠PAQ=∠ABC,
∴△PGA∽△ACB,
∴![]() ,
,
即![]() =3,
=3,
∴![]() ,
,
解得x1=﹣![]() (舍去),x2=0(舍去)
(舍去),x2=0(舍去)
∴此時無符合條件的點P,
綜上所述,存在點P(1,6).


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】為厲行節能減排,倡導綠色出行,今年3月以來.“共享單車”(俗稱“小黃車”)公益活動登陸我市中心城區,某公司擬在甲、乙兩個街道社區投放一批“小黃車”,這批自行車包括A、B兩種不同款型,請回答下列問題:
問題1:單價
該公司早期在甲街區進行了試點投放,共投放A、B兩型自行車各50輛,投放成本共計7500元,其中B型車的成本單價比A型車高10元,A、B兩型自行車的單價各是多少?
問題2:投放方式
該公司決定采取如下投放方式:甲街區每1000人投放a輛“小黃車”,乙街區每1000人投放![]() 輛“小黃車”,按照這種投放方式,甲街區共投放1500輛,乙街區共投放1200輛,如果兩個街區共有15萬人,試求a的值.
輛“小黃車”,按照這種投放方式,甲街區共投放1500輛,乙街區共投放1200輛,如果兩個街區共有15萬人,試求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校科技小組進行野外考察,途中遇到一片濕地,為了安全、迅速通過這片濕地,他們沿著前進路線鋪了若干塊木塊,構筑成一條臨時近道,木板對地面的壓強![]() 是木板面積
是木板面積![]() 的反比例函數,其圖像如下圖所示:
的反比例函數,其圖像如下圖所示:
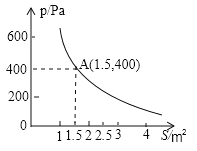
(1)請直接寫出這一函數表達式和自變量取值范圍;
(2)當木板面積為![]() 時,壓強是多少?
時,壓強是多少?
(3)如果要求壓強不超過![]() ,木板的面積至少要多大?
,木板的面積至少要多大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小馬、小虎兩人共同計算一道題:(x+a)(2x+b).由于小馬抄錯了a的符號,得到的結果是2x2﹣7x+3,小虎漏抄了第二個多項式中x的系數得到的結果是x2+2x﹣3.
(1)求a,b的值;
(2)細心的你請計算這道題的正確結果;
(3)當x=﹣1時,計算(2)中的代數式的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
①經過三個點一定可以作圓;②若等腰三角形的兩邊長分別為3和7,則第三邊長是3或7;③一個正六邊形的內角和是其外角和的2倍;④隨意翻到一本書的某頁,頁碼是偶數是隨機事件;⑤關于x的一元二次方程x2-(k+3)x+k=0有兩個不相等的實數根.
A.①②③B.①④⑤C.②③④D.③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A的坐標為(﹣2,0),等邊△AOC經過平移或軸對稱或旋轉都可以得到△OBD.
(1)△AOC沿x軸向右平移得到△OBD,則平移的距離是 個單位長度;△AOC與△BOD關于直線對稱,則對稱軸是 ;△AOC繞原點O順時針旋轉得到△DOB,則旋轉角度可以是 度.
(2)連接AD,交OC于點E,求AD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,O是等邊△ABC內一點,連接OA、OB、OC,且OA=3,OB=4,OC=5,將△BAO繞點B順時針旋轉后得到△BCD,連接OD.求:

①旋轉角的度數;
②線段OD的長;
③∠BDC的度數.
(2)如圖2所示,O是等腰直角△ABC(∠ABC=90°)內一點,連接OA、OB、OC,將△BAO繞點B順時針旋轉后得到△BCD,連接OD.當OA、OB、OC滿足什么條件時,∠ODC=90°?請給出證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程tx26x+m+4=0有兩個實數根x1、x2.
(1)當m=1時,求t的取值范圍;
(2)當t=1時,若x1、x2滿足3| x1|=x2+4,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在《九章算術》“勾股”章中有這樣一個問題:
“今有邑方不知大小,各中開門,出北門二十步有木,出南門十回步,折而西行一千七百七十五步見木.問邑方幾何.”用今天的話說,大意是:如圖,DEFG是一座正方形小城,北門H位于DG的中點,南門K位于EF的中點,出北門20步到A處有一樹木,出南門14步到C,再向西行1775步到B處,正好看到A處的樹木(即點D在直線AB上),求小城的邊長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com