已知:y是x一次函數,且當x=2時,y=-3;且當x=-2時,y=1
(1)試求y與x之間的函數關系式并畫出圖象;
(2)在圖象上標出與x軸、y軸的交點坐標;
(3)當x取何值時,y=5?
【答案】
分析:(1)設y=kx+b(k、b是常數,且k≠0),根據一次函數圖象上點的坐標特征,利用待定系數法求得該函數的解析式;
(2)將x=0,y=0分別代入(1)中的解析式,然后求出該圖象與x軸、y軸的交點坐標分別是(0,-1),(-1,0);
(3)利用(1)的解析式,把y=5代入其中,求出x的值即可.
解答: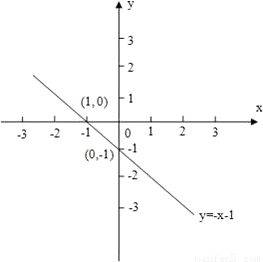
解:(1)設y=kx+b(k、b是常數,且k≠0)
把x=2,y=-3;x=-2,y=1代入
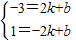
,
解得

,
∴y=-x-1;
(2)當x=0時,y=-1,
當y=0時,x=-1,
所以該圖象與x軸、y軸的交點坐標分別是(0,-1),(-1,0);
(如圖所示)
(3)當y=5時,5=-x-1,
解得,x=-4.
所以當x=-4時,y=5.
點評:本題主要考查了用待定系數法求一次函數的解析式、一次函數的圖象、一次函數圖象坐標上的點的特征.解答此題時,人們往往不注意一次函數的一次項系數k≠0這一條件,所以,在設一次函數解析式y=kx+b時,不要忘記標明(k、b是常數,且k≠0).

 解:(1)設y=kx+b(k、b是常數,且k≠0)
解:(1)設y=kx+b(k、b是常數,且k≠0)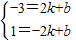 ,
, ,
,

 (北師大版)如圖,已知點A是一次函數y=x的圖象與反比例函數y=
(北師大版)如圖,已知點A是一次函數y=x的圖象與反比例函數y= 如圖,已知點A是一次函數y=2x的圖象與反比例函數y=-
如圖,已知點A是一次函數y=2x的圖象與反比例函數y=- 如圖,已知直線PA是一次函數y=x+n(n>0)的圖象,直線PB是一次函數y=-2x+m(m>n)的圖象.
如圖,已知直線PA是一次函數y=x+n(n>0)的圖象,直線PB是一次函數y=-2x+m(m>n)的圖象.