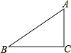
【題目】如圖，在
中．
，
，
，則
A. 
B. 
C. 
D. 
【答案】B
【解析】
本題中直角三角形的角不是特殊角，故過A作AD交BC于D，使∠BAD＝15°，根據三角形內角和定理可求出∠DAC及∠ADC的度數，再由特殊角的三角函數值及勾股定理求解即可．
過A作AD交BC于D，使∠BAD＝15°，
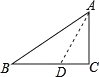
∵△ABC中，∠ACB＝90°，∠ABC＝15°，
∴∠BAC＝75°，
∴∠DAC＝∠BAC∠BAD＝75°15°＝60°，
∴∠ADC＝90°∠DAC＝90°60°＝30°，
∴AC＝
AD，
又∵∠ABC＝∠BAD＝15°
∴BD＝AD，
∵BC＝1，
∴AD＋DC＝1，
CD＝x，則AD＝1x，AC＝（1x），
∴AD2＝AC2＋CD2，即（1x）2＝
（1x）2＋x2，
解得：x＝3＋2
，
∴AC＝（42）＝2，
故選：B．
中考解讀考點精練系列答案科目：初中數學 來源： 題型：
【題目】已知拋物線y=mx2+（2﹣2m）x+m﹣2（m是常數）．
（1）無論m取何值，該拋物線都經過定點 D．直接寫出點D的坐標．
（2）當m取不同的值時，該拋物線的頂點均在某個函數的圖象上，求出這個函數的表達式．
（3）若在0≤x≤1的范圍內，至少存在一個x的值，使y＞0，求m的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，∠ACB＝90°，OC＝2BO，AC＝6，點B的坐標為（1，0），拋物線y＝﹣x2+bx+c經過A、B兩點．
（1）求點A的坐標；
（2）求拋物線的解析式；
（3）點P是直線AB上方拋物線上的一點，過點P作PD垂直x軸于點D，交線段AB于點E，使PE＝
DE．
①求點P的坐標；
②在直線PD上是否存在點M，使△ABM為直角三角形？若存在，求出符合條件的所有點M的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
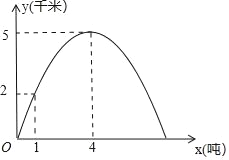
【題目】根據對寧波市相關的市場物價調研，某批發市場內甲種水果的銷售利潤y1（千元）與進貨量x（噸）近似滿足函數關系y1=0.25x，乙種水果的銷售利潤y2（千元）與進貨量x（噸）之間的函數y2=ax2+bx+c的圖象如圖所示．
（1）求出y2與x之間的函數關系式；
（2）如果該市場準備進甲、乙兩種水果共8噸，設乙水果的進貨量為t噸，寫出這兩種水果所獲得的銷售利潤之和W（千元）與t（噸）之間的函數關系式，并求出這兩種水果各進多少噸時獲得的銷售利潤之和最大，最大利潤是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
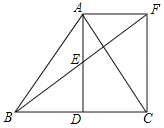
【題目】如圖，△ABC中，D是BC邊上一點，E是AD的中點，過點A作BC的平行線交BE的延長線于F，且AF=CD，連接CF．
（1）求證：△AEF≌△DEB；
（2）若AB=AC，試判斷四邊形ADCF的形狀，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
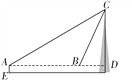
【題目】衡陽市城市標志來雁塔坐落在衡陽市雁峰公園內．如圖，為了測量來雁塔的高度，在E處用高為1.5 m的測角儀AE，測得塔頂C的仰角為30°，再向塔身前進10.4 m，又測得塔頂C的仰角為60°，求來雁塔的高度．(結果精確到0.1 m)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，ABCD中，點E是CD延長線上一點，BE交AD于點F，DE=
CD．
（1）求證：△ABF∽△CEB
（2）若△DEF的面積為2，求ABCD的面積．
（3）若G、H分別為BF、AB的中點，AG、FH交于點O，求
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】省射擊隊為從甲、乙兩名運動員中選拔一人參加全國比賽，對他們進行了六次測試，測試成績如右表(單位：環)：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根據表格中的數據，計算出甲的平均成績是________環，乙的平均成績是________環；
(2)分別計算甲、乙六次測試成績的方差；
(3)根據(1)(2)計算的結果，你認為推薦誰參加全國比賽更合適，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com