
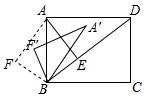
 如圖,矩形ABCD中,AB=2,AD=2$\sqrt{3}$,AE⊥BD,垂足是E,點F是點E關(guān)于AB的對稱點,連接AF、BF,將△ABF繞點B順時針旋轉(zhuǎn)一個α(90°<α<180°)記旋轉(zhuǎn)中的△ABF為△A′B′F′,在旋轉(zhuǎn)過程中,設A′F′所在的直線與直線AD交于點P,與直線BD交于點Q,若△DPQ是等腰三角形,且DP=DQ,則DQ的長為4-$\sqrt{6}$+$\sqrt{2}$.
如圖,矩形ABCD中,AB=2,AD=2$\sqrt{3}$,AE⊥BD,垂足是E,點F是點E關(guān)于AB的對稱點,連接AF、BF,將△ABF繞點B順時針旋轉(zhuǎn)一個α(90°<α<180°)記旋轉(zhuǎn)中的△ABF為△A′B′F′,在旋轉(zhuǎn)過程中,設A′F′所在的直線與直線AD交于點P,與直線BD交于點Q,若△DPQ是等腰三角形,且DP=DQ,則DQ的長為4-$\sqrt{6}$+$\sqrt{2}$. 分析 作輔助線,先根據(jù)勾股定理求出BD的長,由直角三角形斜邊是直角邊的2倍,則這條直角邊的所對的銳角為30°,求出∠ADB=30°,再由對稱和旋轉(zhuǎn)可得:∠A′=30°,從而根據(jù)所作的高線得:△BGM是等腰直角三角形,并根據(jù)等腰三角形的性質(zhì)依次求出∠DPQ=∠DQP=75°,由矩形的對邊平行得:AD∥BC,
根據(jù)平行線的內(nèi)錯角相等可知∠BMP=∠DPQ=75°,所以∠BQM=∠BMP=75°,設BG=x,則GM=x,A′M=2x,A′G=$\sqrt{3}$x,根據(jù)A′B=2,列方程解出可得結(jié)論.
解答 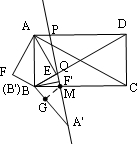 解:如圖所示,當DP=DQ時,∠DPQ=∠DQP,
解:如圖所示,當DP=DQ時,∠DPQ=∠DQP,
設A′P與BC交于M,過M作MG⊥A′B于G,
∵四邊形ABCD為矩形,
∴∠BAD=90°,
∵AB=2,AD=2$\sqrt{3}$,
由勾股定理得:BD=4,
∴BD=2AB,
∴∠ADB=30°,∠ABD=60°,
∵AE⊥BD,
∴∠AEB=90°,
∴∠BAE=30°,
由對稱得:∠FAB=∠EAB=30°,
由旋轉(zhuǎn)得:△A′BF′≌△ABF≌△EAB,
∴A′B=AB=2,∠A′=∠BAF=30°,
∵∠ADB=30°,
∴∠DPQ=∠DQP=75°,
∵AD∥BC,
∴∠BMP=∠DPQ=75°,
∴∠BQM=∠BMP=75°,
∴BQ=BM,
∴∠GBM=75°-30°=45°,
∴△BGM是等腰直角三角形,
∴BG=GM,
設BG=x,則GM=x,A′M=2x,A′G=$\sqrt{3}$x,
∵A′B=2,
∴BG+A′G=2,
x+$\sqrt{3}$x=2,
x=$\sqrt{3}$-1,
∴BM=$\sqrt{2}$x=$\sqrt{2}$($\sqrt{3}$-1)=$\sqrt{6}$-$\sqrt{2}$,
∴DQ=BD-BQ=BD-BM=4-($\sqrt{6}$-$\sqrt{2}$)=4-$\sqrt{6}$+$\sqrt{2}$;
故答案為:4-$\sqrt{6}$+$\sqrt{2}$.
點評 本題考查了矩形的性質(zhì)、旋轉(zhuǎn)和軸對稱的性質(zhì)、等腰直角三角形的性質(zhì)和判定、直角三角形30°角的性質(zhì)和判定等知識,應用的知識點較多,本題的突破口是根據(jù)已知所構(gòu)成的等腰三角形正確畫出圖形,根據(jù)等腰三角形的等邊對等角以及旋轉(zhuǎn)的性質(zhì)得出相應的角和邊相等是關(guān)鍵,與勾股定理結(jié)合,使問題得以解決.


 精英口算卡系列答案
精英口算卡系列答案科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | x=-1或x=1 | B. | x=0 | C. | x=1 | D. | x=-1 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=2或-2,b=3 | D. | a=0,b=3 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | -2 | B. | 0 | C. | $\sqrt{2}$ | D. | 3 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com