【題目】用適當的方法解下列方程
（1）
（2）
（3）
（4）
【答案】（1）
；（2）
；（3）
；（4）
．
【解析】
（1）先移項，然后用直接開平方法求解；
（2）用求根公式法求解；
（3）移項，然后用因式分解法求解；
（4）用多項式乘以多項式打開括號，移項，用因式分解法求解．
（1）移項得：（x+3）2=25，
開方：x+3=±5，
即：x+3=5，x+3=-5，
解得：x1=2，x2=-8；
（2）由題意得：a=2，b=4，c=1，Δ=16-8=8>0，
所以方程有兩個不相等的實數根，
所以x=
，
所以x1=
，x2=
；
（3）移項得：3（x-2）2-x（x-2）=0，
因式分解得：[3（x-2）-x]（x-2）=0，即（2x-6）（x-2）=0，
解得：x1=3，x2=2；
（4）去括號整理得：x2+9x+8=-12，
x2+9x+20=0，
因式分解得：（x+4）（x+5）=0，
解得：x1=-4，x2=-5.
互動課堂系列答案
激活思維智能訓練課時導學練系列答案科目：初中數學 來源： 題型：
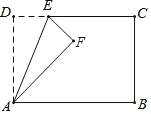
【題目】如圖，在矩形ABCD中，AD=5，AB=8，點E為射線DC上一個動點，把△ADE沿直線AE折疊，當點D的對應點F剛好落在線段AB的垂直平分線上時，則DE的長為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小林準備進行如下操作試驗：把一根長為
的鐵絲剪成兩段，并把每一段各圍成一個正方形．
（1）要使這兩個正方形的面積之和等于
，小林該怎么剪？
（2）小峰對小林說：“這兩個正方形的面積之和不可能等于
．”他的說法對嗎？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】操作：
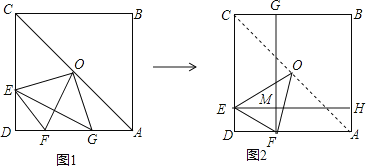
如圖1，正方形ABCD中，AB=a，點E是CD邊上一個動點，在AD上截取AG=DE，連接EG，過正方形的中線O作OF⊥EG交AD邊于F，連接OE、OG、EF、AC．
探究：
在點E的運動過程中：
（1）猜想線段OE與OG的數量關系？并證明你的結論；
（2）∠EOF的度數會發生變化嗎？若不會，求出其度數，若會，請說明理由．
應用：
（3）當a=6時，試求出△DEF的周長，并寫出DE的取值范圍；
（4）當a的值不確定時：
①若
=
時，試求
的值；
②在圖1中，過點E作EH⊥AB于H，過點F作FG⊥CB于G，EH與FG相交于點M；并將圖1簡化得到圖2，記矩形MHBG的面積為S，試用含a的代數式表示出S的值，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
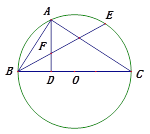
【題目】如圖，已知BC是⊙O的直徑，A是⊙O上一點，AD⊥BC，垂足為D，
＝
，BE交AD于點F．
（1）∠ACB與∠BAD相等嗎？為什么？
（2）判斷△FAB的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，邊長為2的等邊三角形AEF的頂點E、F分別在BC和CD上．下列結論：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=2+
．其中正確結論的序號是________________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】中學生上學帶手機的現象越來越受到社會的關注，為此媒體記者隨機調查了某校若干名學生上學帶手機的目的，分為四種類型：A接聽電話；B收發短信；C查閱資料；D游戲聊天．并將調查結果繪制成圖1和圖2的統計圖（不完整），請根據圖中提供的信息，解答下列問題：
（1）此次抽樣調查中，共調查了 名學生；
（2）將圖1、圖2補充完整；
（3）現有4名學生，其中A類兩名，B類兩名，從中任選2名學生，求這兩名學生為同一類型的概率（用列表法或樹狀圖法）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，△ABC的三個頂點坐標分別為A（1，4），B（4，2），C（3，5）（每個方格的邊長均為1個單位長度）．
（1）請畫出將△ABC向下平移5個單位后得到的△A1B1C1；
（2）將△ABC繞點O逆時針旋轉90°，畫出旋轉后得到的△A2B2C2，并直接寫出點B旋轉到點B2所經過的路徑長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com