
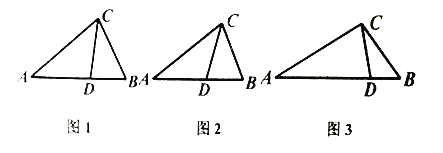
【題目】從三角形(不是等腰三角形)一個頂點引出一條射線 與對邊相交,頂點與交點之間的線段把這個三角形分割成兩個小三角形,如果分得的兩個小三角形中一個為等腰三角形,另一個與原三角形相似,我們把這條線段叫做這個三角形的完美分割線.
![]() 如圖1,在
如圖1,在![]() 中,
中,![]() 是
是![]() 的完美分割線,且
的完美分割線,且![]() , 則
, 則![]() 的度數是
的度數是
![]() 如圖2,在
如圖2,在![]() 中,
中,![]() 為角平分線,
為角平分線,![]() ,求證:
,求證: ![]() 為
為![]() 的完美分割線.
的完美分割線.
![]() 如圖2,
如圖2,![]() 中,
中,![]() 是
是![]() 的完美分割線,且
的完美分割線,且![]() 是以
是以![]() 為底邊的等腰三角形,求完美分割線
為底邊的等腰三角形,求完美分割線![]() 的長.
的長.
科目:初中數學 來源: 題型:
【題目】定義:在平面直角坐標系中,我們將函數![]() 的圖象繞原點
的圖象繞原點![]() 逆時針旋轉
逆時針旋轉![]() 后得到的新曲線
后得到的新曲線![]() 稱為“逆旋拋物線”.
稱為“逆旋拋物線”.
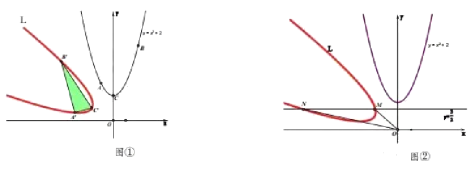
(1)如圖①,己知點![]() ,
,![]() 在函數
在函數![]() 的圖象上,拋物線的頂點為
的圖象上,拋物線的頂點為![]() ,若
,若![]() 上三點
上三點![]() 、
、![]() 、
、![]() 是
是![]() 、
、![]() 、
、![]() 旋轉后的對應點,連結
旋轉后的對應點,連結![]() ,
,![]() 、
、![]() ,則
,則![]() __________;
__________;
(2)如圖②,逆旋拋物線![]() 與直線
與直線![]() 相交于點
相交于點![]() 、
、![]() ,則
,則![]() __________.
__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
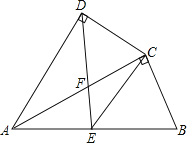
【題目】如圖,四邊形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E為AB的中點,
(1)求證:AC2=ABAD.
(2)求證:CE∥AD;
(3)若AD=4,AB=6,求AF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,拋物線y=ax2+3ax+c(a>0)與y軸交于點C,與x軸交于A,B兩點,點A在點B左側.點B的坐標為(1,0),OC=3OB,
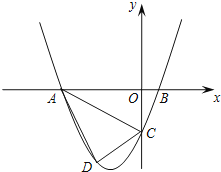
(1)求拋物線的解析式;
(2)若點D是線段AC下方拋物線上的動點,求四邊形ABCD面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
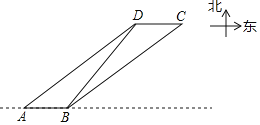
【題目】如圖為某海域示意圖,其中燈塔D的正東方向有一島嶼C.一艘快艇以每小時20nmile的速度向正東方向航行,到達A處時得燈塔D在東北方向上,繼續航行0.3h,到達B處時測得燈塔D在北偏東30°方向上,同時測得島嶼C恰好在B處的東北方向上,此時快艇與島嶼C的距離是多少?(結果精確到1nmile.參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題發現
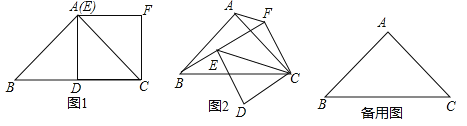
如圖1,在![]() 中,
中,![]() ,點
,點![]() 為
為![]() 的中點,以
的中點,以![]() 為一邊作正方形
為一邊作正方形![]() ,點
,點![]() 恰好與點
恰好與點![]() 重合,則線段
重合,則線段![]() 與
與![]() 的數量關系為______________;
的數量關系為______________;
(2)拓展探究
在(1)的條件下,如果正方形![]() 繞點
繞點![]() 旋轉,連接
旋轉,連接![]() ,線段
,線段![]() 與
與![]() 的數量關系有無變化?請僅就圖2的情形進行說明;
的數量關系有無變化?請僅就圖2的情形進行說明;
(3)問題解決.
當正方形![]() 旋轉到
旋轉到![]() 三點共線時,直接寫出線段
三點共線時,直接寫出線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
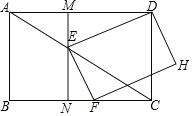
【題目】如圖,在矩形ABCD中,AB=3,BC=4,點E是線段AC上的一個動點且![]() =k(0<k<1),點F在線段BC上,且DEFH為矩形;過點E作MN⊥BC,分別交AD,BC于點M,N.
=k(0<k<1),點F在線段BC上,且DEFH為矩形;過點E作MN⊥BC,分別交AD,BC于點M,N.
(1)求證:△MED∽△NFE;
(2)當EF=FC時,求k的值.
(3)當矩形EFHD的面積最小時,求k的值,并求出矩形EFHD面積的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國慶期間,某風景區推出兩種旅游觀光活動付費方式:若人數不超過20人,人均繳費500元;若人數超過20人,則每增加一位旅客,人均收費降低10元,但是人均收費不低于350元.現在某單位在國慶期間組織一批貢獻突出的職工到該景區旅游觀光,支付了12000元觀光費,請問:該單位一共組織了多少位職工參加旅游觀光活動?
查看答案和解析>>
科目:初中數學 來源: 題型:
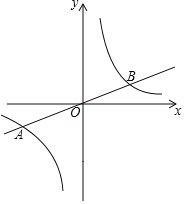
【題目】如圖,正比例函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于
的圖象交于![]() 、
、![]() 兩點.
兩點.![]() 是第一象限內反比例函數圖象上一點,過點
是第一象限內反比例函數圖象上一點,過點![]() 作
作![]() 軸的平行線,交直線
軸的平行線,交直線![]() 于點
于點![]() ,連接
,連接![]() ,若
,若![]() 的面積為
的面積為![]() ,則點
,則點![]() 的坐標為_____________.
的坐標為_____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com