
【題目】如圖,某市為方便行人過馬路,打算修建一座高為4x(m)的過街天橋.已知天橋的斜面坡度i=1:0.75是指坡面的鉛直高度DE(CF)與水平寬度AE(BF)的比,其中DC∥AB,CD=8x(m).
(1)請求出天橋總長和馬路寬度AB的比;
(2)若某人從A地出發,橫過馬路直行(A→E→F→B)到達B地,平均速度是2.5m/s;返回時從天橋由BC→CD→DA到達A地,平均速度是1.5m/s,結果比去時多用了12.8s,請求出馬路寬度AB的長.
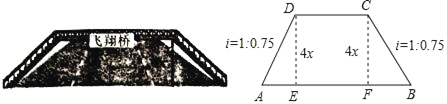
【答案】(1)9:7;(2)AB的長為28m.
【解析】
(1)先證明四邊形CDEF是矩形,得EF=DC=8x,根據坡度的定義可得EA=BF=3x,AD=BC=5x,所以AB=AE+EF+BF=14x,天橋總長和馬路寬度AB的比=18x:14x.(2) 由(1)可知,AB=14x,AD+CD+BC=18x,由題意:![]() ,解方程可得.
,解方程可得.
解:(1)∵DE⊥AB,CF⊥AB,
∴∠DEF=∠CFE=90°,
∴DE∥CF,
∵DC∥AB,
∴四邊形CDEF是矩形,
∴EF=DC=8x,
∵![]() =
=![]() =
=![]() ,
,
∴EA=BF=3x,
∴AD=BC=5x,
∴AB=AE+EF+BF=14x,
∴天橋總長和馬路寬度AB的比=18x:14x=9:7.
(2)由(1)可知,AB=14x,AD+CD+BC=18x,
由題意:![]() =
=![]() ﹣12.8,
﹣12.8,
解得x=2,
∴14x=28,
答:馬路寬度AB的長為28m.


科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜邊AB上的中線,將△BCD沿直線CD翻折至△ECD的位置,連接AE.若DE∥AC,計算AE的長度等于_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,禁止捕魚期間,某海上稽查隊在某海域巡邏,上午某一時刻在A處接到指揮部通知,在他們東北方向距離12海里的B處有一艘捕魚船,正在沿南偏東75°方向以每小時10海里的速度航行,稽查隊員立即乘坐巡邏船以每小時14海里的速度沿北偏東某一方向出發,在C處成功攔截捕魚船,則巡邏船從出發到成功攔截捕魚船所用的時間是( )

A. 1小時 B. 2小時 C. 3小時 D. 4小時
查看答案和解析>>
科目:初中數學 來源: 題型:
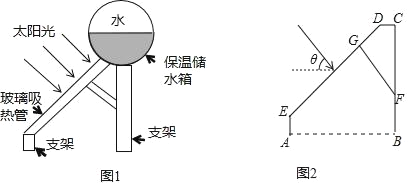
【題目】圖1是太陽能熱水器裝置的示意圖,利用玻璃吸熱管可以把太陽能轉化為熱能,玻璃吸熱管與太陽光線垂直時,吸收太陽能的效果最好,假設某用戶要求根據本地區冬至正午時刻太陽光線與地面水平線的夾角(θ)確定玻璃吸熱管的傾斜角(太陽光線與玻璃吸熱管垂直),請完成以下計算:如圖2,AB⊥BC,垂足為點B,CD∥AB,FG⊥DE,垂足為點G,若∠θ=37°50′,FG=30cm,CD=10cm,求CF的長(結果取整數,參考數據:sin37°50′≈0.6l,cos37°50′≈079,tan37°50′≈0.78)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家食品公司將一種新研發的食品免費送給一些人品嘗,并讓每個人按A(不喜歡)、B(一般)、C(比較喜歡)、D(非常喜歡)四個等級對食品進行評價,圖1和圖2是該公司采集數據后,繪制的兩幅不完整的統計圖.
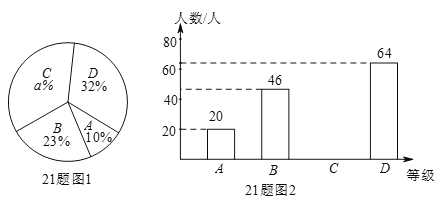
請你根據以上統計圖提供的信息,回答下列問題:
(1)本次調查的人數為 人;
(2)圖1中,a = ,C等級所占的圓心角的度數為 度;
(3)請直接在圖中補全條形統計圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
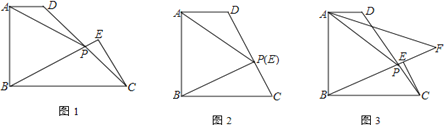
【題目】如圖1,在直角梯形ABCD中,AB⊥BC,AD∥BC,點P為DC上一點,且AP=AB,過點C作CE⊥BP交直線BP于E.
(1) 若![]() ,求證:
,求證:![]() ;
;
(2) 若AB=BC.
① 如圖2,當點P與E重合時,求![]() 的值;
的值;
② 如圖3,設∠DAP的平分線AF交直線BP于F,當CE=1,![]() 時,直接寫出線段AF的長.
時,直接寫出線段AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個正方形AOBC各頂點的坐標分別為A(0,3),O(0,0),B(3,0),C(3,3).若以原點為位似中心,將這個正方形的邊長縮小為原來的![]() ,則新正方形的中心的坐標為_____.
,則新正方形的中心的坐標為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com