
 如圖,在Rt△ABC中,∠B=90°,AB=3,AC=5,點(diǎn)E在BC上,將△ABC沿AE折疊,使點(diǎn)B落在AC邊上的點(diǎn)B′處,則BE的長為( )
如圖,在Rt△ABC中,∠B=90°,AB=3,AC=5,點(diǎn)E在BC上,將△ABC沿AE折疊,使點(diǎn)B落在AC邊上的點(diǎn)B′處,則BE的長為( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
分析 利用勾股定理求出BC=4,設(shè)BE=x,則CE=4-x,在Rt△B'EC中,利用勾股定理列方程,解出x的值即可.
解答  解:∵Rt△ABC中,∠B=90°,AB=3,AC=5,
解:∵Rt△ABC中,∠B=90°,AB=3,AC=5,
∴BC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
由折疊的性質(zhì)得:BE=BE′,AB=AB′,
設(shè)BE=x,則B′E=x,CE=4-x,
B′C=AC-AB′=5-3=2,
在Rt△B′EC中,B′E2+B′C2=EC2,
即x2+22=(4-x)2,
解得x=$\frac{3}{2}$,
即BE的長為$\frac{3}{2}$.
故選:C.
點(diǎn)評(píng) 本題考查了翻折變換以及勾股定理的運(yùn)用,解答本題的關(guān)鍵是掌握翻折變換的性質(zhì)及運(yùn)用勾股定理的表達(dá)式列出方程求解.


 名牌學(xué)校分層周周測系列答案
名牌學(xué)校分層周周測系列答案 黃岡海淀全程培優(yōu)測試卷系列答案
黃岡海淀全程培優(yōu)測試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
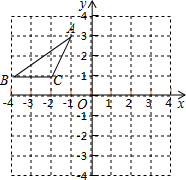 如圖,在平面直角坐標(biāo)系中,點(diǎn)A、B、C的坐標(biāo)分別為(-1,3)、(-4,1)、(-2,1),先將△ABC沿一確定方向平移得到△A1B1C1,點(diǎn)B的對(duì)應(yīng)點(diǎn)B1的坐標(biāo)是(1,2),再將△A1B1C1繞原點(diǎn)O順時(shí)針旋轉(zhuǎn)90°得到△A2B2C2,點(diǎn)A1的對(duì)應(yīng)點(diǎn)為點(diǎn)A2.
如圖,在平面直角坐標(biāo)系中,點(diǎn)A、B、C的坐標(biāo)分別為(-1,3)、(-4,1)、(-2,1),先將△ABC沿一確定方向平移得到△A1B1C1,點(diǎn)B的對(duì)應(yīng)點(diǎn)B1的坐標(biāo)是(1,2),再將△A1B1C1繞原點(diǎn)O順時(shí)針旋轉(zhuǎn)90°得到△A2B2C2,點(diǎn)A1的對(duì)應(yīng)點(diǎn)為點(diǎn)A2.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,直線y=-x+2與x軸、y軸分別交于點(diǎn)A,B,點(diǎn)C在x軸上,∠α=75°,則點(diǎn)C 的坐標(biāo)是( )
如圖,直線y=-x+2與x軸、y軸分別交于點(diǎn)A,B,點(diǎn)C在x軸上,∠α=75°,則點(diǎn)C 的坐標(biāo)是( )| A. | (-2$\sqrt{3}$,0) | B. | (-4,0) | C. | (-$\frac{2\sqrt{3}}{3}$,2) | D. | (-2,0) |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com